Introdução

Este curso tem como objetivo propagar as ideias básicas de aprendizado de máquina e previsão no software estatístico R. A ideia principal é cobrir as técnicas mais usadas como regressão linear, árvores de decisão, e também detalhes básicos e aspectos práticos do aprendizado de máquina. Inicialmente será utilizado alguns códigos básicos do R para alguns modelos de previsão. Contudo, o foco principal será no pacote caret, o qual tem a finalidade de tornar as técnicas de aprendizado mais simples, combinando um grande número de preditores que foram construídos no R.

Pré-requisitos

Os pré-requisitos que serão úteis para o curso são: análise exploratória de dados no R, programação básica em R e conhecimentos teóricos básicos sobre modelos de regressão.

O que é o Aprendizado de Máquina?

Em 1959, Arthur Samuel definiu o aprendizado de máquina como o “campo de estudo que dá aos computadores a habilidade de aprender sem serem explicitamente programados”. Ou seja, é um método de análise de dados que automatiza a construção de modelos analíticos. É baseado na ideia de que sistemas podem aprender com dados, identificar padrões e tomar decisões com o mínimo de intervenção humana. A importância desse aprendizado se deve principalmente ao fato de que atualmente tem surgido cada vez mais a necessidade de manipulações de grandes volumes e variedades de dados disponíveis.

Para que serve?

Com o aprendizado de máquina é possível produzir, rápida e automaticamente, modelos capazes de analisar dados maiores e mais complexos, e entregar resultados mais rápidos e precisos – mesmo em grande escala.

Onde é usado?

Ao construir modelos precisos há mais chances de identificar boas oportunidades e de evitar riscos desconhecidos. Na prática, podemos citar alguns exemplos reais do uso de aprendizado de máquina:

• Os governos locais podem tentar prever os pagamentos de pensão no futuro para que eles saibam se seus mecanismos de geração de receita têm fundos suficientes gerados para cobrir esses pagamentos de pensão.
• O Google pode querer prever se você vai clicar em um anúncio para que ele possa mostrar apenas os anúncios com maior probabilidade de receber cliques e, assim, aumentar a receita.
• A Amazon, a Netflix e outras empresas como essa mostram um filme e querem que você veja um próximo filme. Para fazer isso, eles querem mostrar a você o que você pode estar interessado, para que eles possam mantê-lo assistindo e, novamente, aumentar a receita.
• As seguradoras empregam grandes grupos de atuários e estatísticos para tentar prever seu risco de todo tipo de coisas diferentes, como por exemplo a morte.

Como funciona?

A funcionalidade do aprendizado de máquina se resume a tentar prever um certo modelo para o conjunto de dados em questão. Há dois modos de isso ser feito: pelo aprendizado supervisionado e pelo aprendizado não supervisionado. Veremos a definição de cada um deles a seguir.

Tipos de Aprendizado de Maquina

Aprendizado não supervisionado

Na aprendizagem não supervisionada, temos um conjunto de dados não rotulados e queremos de alguma forma agrupá-los por um certo padrão encontrado. Vejamos alguns exemplos:

• Exemplo 1: Dada uma imagem de homem/mulher, temos de prever sua idade com base em dados da imagem.
• Exemplo 2: Dada as informações sobre que músicas uma pessoa costuma ouvir, sugerir outras que possam agradá-la também.

Aprendizado supervisionado

No aprendizado supervisionado, por outro lado, temos um conjunto de dados já rotulados que sabemos qual é a nossa saída correta e que deve ser semelhante ao conjunto. Queremos assim, com base nesses dados, ser capaz de classificar outros dados do mesmo tipo e que ainda não foram rotulados.

• Exemplo 1: Dada uma coleção de 1000 pesquisas de uma universidade, encontrar uma maneira de agrupar automaticamente estas pesquisas em grupos que são de alguma forma semelhantes ou relacionadas por diferentes variáveis, tais como a frequência das palavras, frases, contagem de páginas, etc.
• Exemplo 2: Dada uma grande amostra de e-mails, encontrar uma maneira de agrupá-los automaticamente em “spam” ou “não spam”, de acordo com as características das palavras, tais como a frequência com que uma certa palavra aparece, a frequência de letras maiúsculas, de cifrões ($), entre outros.

Se os valores da variável rótulo, também chamada de variável de interesse, são valores discretos finitos ou ainda categóricos, então temos um problema de classificação e o algoritmo que criaremos para resolver nosso problema será chamado Classificador.

Se os valores da Variável de Interesse são valores contínuos, então temos um problema de regressão e o algoritmo que criaremos será chamado Regressor.

A aprendizagem supervisionada será o principal foco do curso.

---

Predição

Queremos então construir um algoritmo “preditor” capaz de inferir se um dado pertence ou não a uma certa categoria. O preditor será formado dos seguintes componentes:

Pergunta \(\rightarrow\) Amostra de entrada \(\rightarrow\) Características \(\rightarrow\) Algoritmo \(\rightarrow\) Parâmetros \(\rightarrow\) Avaliação

Pergunta

O nosso objetivo é responder a uma pergunta de tipo “O dado A é do tipo x ou do tipo y?”. Por exemplo, podemos querer saber se é possível detectar automaticamente se um e-mail é um spam ou um “ham”, isto é, não spam. O que na verdade queremos saber é: “É possível usar características quantitativas para classificar um e-mail como spam?”.

Amostra de Entrada

Uma vez formulada a pergunta, precisamos obter uma amostra de onde tentaremos extrair informações que caracterizam a categoria a qual um dado pertence e então usar essas informações para classificar outros dados não categorizados. O ideal é que se tenha uma amostra grande, assim teremos melhores parâmetros para construir nosso preditor.

No caso da pergunta sobre um e-mail ser spam ou não, temos acesso a base de dados “spam” disponível no pacote “kernlab”, onde cada linha dessa base é um e-mail e nas colunas temos a porcentagem de palavras e números contidos em cada e-mail e, entre outras coisas, a nossa variável de interesse “type” que classifica o e-mail como spam ou não:

library(kernlab)
data(spam)
head(spam)

Obtida a amostra, precisamos dividi-la em duas partes que chamaremos de Conjunto de Treino e Conjunto de Teste. O conjunto de treino será usado para construir o algoritmo. É dele que vamos extrair as informações que julgarmos utéis para classificar uma categoria de dado. É importante que o modelo de previsão seja feito com base apenas no conjunto de treino.

set.seed(127)
indices = sample(dim(spam)[1], size = 2760)
treino = spam[indices,]
teste = spam[-indices,]

Após construido o algoritmo, usaremos o conjunto de teste para obter a estimativa de erro, que será detalhada mais a frente.

Características

Temos que encontrar agora características que possam indicar a categoria dos dados. Podemos, por exemplo, vizualizar algumas variáveis graficamente para obter uma ideia do que podemos fazer. No nosso exemplo de e-mails, podemos querer avaliar se a frequência de palavras “your” em um e-mail pode indicar se ele é um spam ou não.

plot(density(treino$your[treino$type=="nonspam"]), col="blue", 
     main = "Densidade de 'your' em ham (azul) e spam (vermelho)", 
     xlab = "Frequência de 'your'", ylab = "densidade")
lines(density(treino$your[treino$type=="spam"]), col="red")

Pelo gráfico podemos notar que a maioria dos e-mails que são spam têm uma frequência maior da palavra “your”. Por outro lado, aqueles que são classificados como ham (não spam) têm um pico mais alto perto do 0.

Algoritmo

Com base nisso podemos construir um algoritmo para prever se um e-mail é spam ou ham. Podemos estimar um modelo onde queremos encontrar uma constante c tal que se a frequência da palavra “your” for maior que c, então classificamos o e-mail como spam. Caso contrário, classificamos o e-mail como não spam.

Vamos observar graficamente como ficaria esse modelo se c=0.8.

plot(density(treino$your[treino$type=="nonspam"]), col="blue", 
     main = "Densidade de 'your' em ham (azul) e spam (vermelho)", 
     xlab = "Frequência de 'your'", ylab = "densidade")
lines(density(treino$your[treino$type=="spam"]), col="red")
abline(v=0.8,col="black")

Os e-mails à direita da linha preta seriam classificados como spam, enquanto que os à esquerda seriam classificados como não spam.

Avaliação

Agora vamos avaliar nosso modelo de predição.

predicao=ifelse(treino$your>0.8,"spam","nonspam")
table(predicao,treino$type)/length(treino$type)

Podemos ver que quando os e-mails não eram spam e classificamos como “não spam”, de acordo com nosso modelo, em 50% do tempo nós acertamos. Quando os e-mails eram spam e classificamos ele em spam, por volta de 26% do tempo nós acertamos. Então, ao total, nós acertamos por volta de 50+26=76% do tempo. Então nosso algoritmo de previsão tem uma precisão por volta de 76% na amostra treino.

predicao=ifelse(teste$your>0.8,"spam","nonspam")
table(predicao,teste$type)/length(teste$type)

Já na amostra teste acertamos 48+27=75% das vezes. O erro na amostra teste é o que chamamos de erro real. É o erro que esperamos em amostras novas que passarem por nosso preditor.

Como construir um bom algoritmo de aprendizado de máquina?

O “melhor” método de aprendizado de máquina é caracterizado por:

• Uma boa base de dados;
• Reter informações relevantes;
• Ser bem interpretável;
• Fácil de ser explicado e entendido;
• Ser preciso;
• Fácil de se construir e de se testar em pequenas amostras;
• Fácil aplicar a um grande conjunto de dados.

Os erros mais comuns, que se deve tomar um certo cuidado, são:

• Tentar automatizar a seleção de variáveis (características) de uma maneira que não permita que você entenda como essas variáveis estão sendo aplicadas para fazer previsões;
• Não prestar atenção a peculiaridades específicas de alguns dados, como comportamentos estranhos de variáveis específicas;
• Jogar fora informações desnecessariamente.

---

Design de predição

1. Defina sua taxa de erro (benchmark).

Por hora iremos utilizar uma taxa de erro genérica, mas em um próximo iremos falar sobre quais são as diferentes taxas de erro possíveis que você pode escolher.

Por exemplo, podemos calcular o chamado erro majoritário que é o limite máximo abaixo do qual o erro de um classificador deve estar. Ele é dado por \(1-p\), onde \(p\) é a proporção da categoria mais requente na variável de interesse. Por exemplo, se a variável de interesse possui 2 categorias: A e B. Se \(85\%\) dos dados estão rotulados na categoria A e \(15\%\) na categoria B, entao temos que a categoria A é a classe majoritária e \(100\%-85\% = 15\%\) é o erro majoritário.

Caso o erro do preditor seja superior ao erro majoritário, seria melhor classificar toda nova amostra na classe majoritária, certo? Depende.

Digamos que um psicólogo quer construir um classificador para prever se uma pessoa tem ou não indeação suicida, ou seja, pensa ou planeja suicídio. Suponha que ele tem uma base de dados com 1000 observações cuja variável de interesse “Tem indeação suicida?” está rotulada com “sim” ou “não” e 97% das observações, no caso indivíduos/pacientes, não possuem tal característica e portanto 3% dos indivíduos possuem. Criado o preditor, observamos que o erro é de 5%, assim como mostrado a seguir:

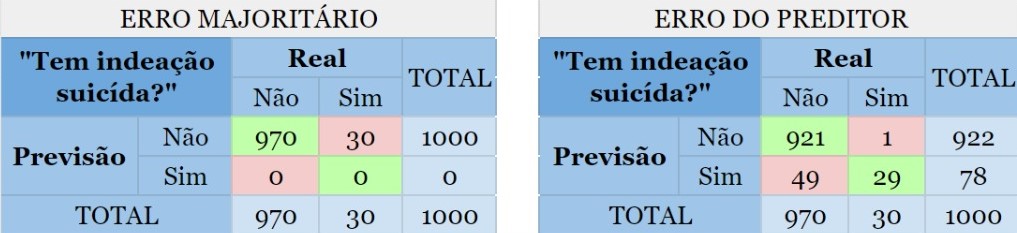
{width=95%}

As partes em vermelho mostram o erro cometido por ambos os métodos. Agora note as pessoas que possuem indeação suicída porém foram classficadas como não possuidoras dessa característica. Quanto isso afetará no dignóstico do psicólogo?

2. Divida os dados em Treino e Teste, ou Treino, Teste e Validação (opcional).

Como já comentado, o conjunto de treino deve ser criado para construir seu modelo e o conjunto de testes para avaliar seu modelo. Fazemos isso com o intuito de criarmos um modelo que se ajuste bem a qualquer base de dados, e não apenas à nossa. É comum usar 70% da amostra como treino e 30% como teste, mas isso não é uma regra. Podemos também repartir os dados em treino, teste e validação(*). É importante ficar claro que quem está conduzindo as análises é quem fica encarregado de decidir o que fica melhor para cada amostra.

3. Definimos quais variáveis serão utilizadas para estimação dos parâmetros do classificador/regressor (função preditora).

Nem sempre utilizar todas as variáveis do banco de dados é importante para o modelo. Pode acontecer de termos variáveis que não ajudam na predição, como por exemplo aquelas com uma variância quase zero (frequência muito alta de um único valor). Iremos estudar algumas formas de selecionar as melhores variáveis para o modelo em breve.

4. Definimos o método que será utilizado para construção do classificador/regressor.

Isso poderá ser feito, por exemplo, utilizando o método de validação cruzada (cross-validation), que será explicado detalhadamente em um capítulo mais à frente.

5. Utilizando a amostra TREINO, definimos os parâmetros da função preditora (classificador/regressor), obtendo o melhor modelo possível.

6. Aplicamos o melhor modelo obtido na amostra TESTE uma única vez, para estimar o erro do preditor.

Aplicamos o melhor modelo na amostra teste apenas uma vez porque se aplicarmos diversas vezes até achar o melhor modelo estaremos utilizando o teste, de certa forma, para treinar o modelo, pois o ajuste do modelo seria influenciado pelo resultado do teste. Isso não é desejável pois o objetivo do teste é nos servir como uma “nova amostra”.

() Opcionalmente poderá ser criado um conjunto de **validação*, com o intuito de servir como um “pré-teste”, que também será usado para avaliar seu modelo. Quando repartimos o conjunto de dados dessa forma, utilizamos o treino para construir o modelo, avaliamos o modelo na validação (ou seja, o ajuste do modelo é influenciado por ela), e se o resultado não for bom, retornamos ao teste para ajustar um outro modelo. Então novamente testamos o modelo na validação, e assim sucessivamente até acharmos um modelo que se adequou bem tanto ao treino quanto à validação. Aí, finalmente, aplicamos ele ao conjunto teste, avaliando na prática a sua qualidade.

---

Erros Amostrais

Este é um dos conceitos mais fundamentais com os quais lidamos na aprendizagem de máquina e previsão. Temos duas taxas de erros amostrais: o erro dentro da amostra (in sample error) e o erro fora da amostra (out of sample error).

Erro dentro da Amostra (In Sample Error)

É a taxa de erro que você recebe no mesmo conjunto de dados usado para criar seu preditor. Na literatura às vezes é chamado de erro de resubstituição. Em outras palavras, é quando seu algoritmo de previsão se ajusta um pouco ao que você coletou num conjunto de dados específico. E assim, quando você recebe um novo conjunto de dados, a precisão diminuirá um pouco.

Erro fora da Amostra (Out of Sample Error)

É a taxa de erro que você recebe em um novo conjunto de dados. Na literatura às vezes é chamado de erro de generalização. A ideia é que uma vez que coletamos uma amostra de dados e construímos um modelo para ela, podemos querer testá-lo em uma nova amostra, por exemplo uma amostra coletada por uma pessoa diferente ou em um horário diferente. Daí podemos analisar o quão bem o algoritmo executará a predição nesse novo conjunto de dados.

Algumas ideias-chave {#link4}

1. Quase sempre o erro fora da amostra é o que interessa.
2. Erro dentro da amostra é menor que o erro fora da amostra.
3. Um erro frequente é ajustar muito o algoritmo ao dados que temos. Em outras palavras, criar um modelo overfitting(*).

(*) Overfitting é um termo usado na estatística para descrever quando um modelo estatístico se ajusta muito bem a um conjunto de dados anteriormente observado e, como consequência, se mostra ineficaz para prever novos resultados.

Vejamos um exemplo de erro dentro da amostra vs erro fora da amostra:

set.seed(333)

#Vamos selecionar as linhas da base de dados spam através de uma amostra de tamanho 10 das 4601 linhas
# dos dados:
spamMenor=spam[sample(dim(spam)[1],size=10), ]

#Vamos criar um vetor composto pelos rótulos "1" e "2". 
#Se um e-mail da nossa amostra for spam, recebe "1", se não for spam, recebe "2".
spamRotulos=(spamMenor$type=="spam")*1 + 1

#Na nossa base: capitalAve = média de letras maiúsculas por linha.
plot(spamMenor$capitalAve,col=spamRotulos,xlab="Quantidade de Letras Maiúsculas",
     ylab="Frequência",main="Letras Maiúsculas em spam (vermelho) e em ham (preto)", pch=19)

Podemos notar que as mensagens classificadas como spam possuem uma frequência maior de letras maiúsculas do que as mensagens classificadas como não spam. Com base nisso queremos construir um preditor, onde podemos classificar e-mails como spam se a frequência de letras maiúsculas for maior que uma determida constante, e não spam caso contrário.

Veja que se separarmos os dados pela frequência de letras maiúsculas maior que 2.9 e classificarmos o que esta acima como spam e abaixo como não spam, ainda temos uma observação spam abaixo da linha.

plot(spamMenor$capitalAve,col=spamRotulos,xlab="Quantidade de Letras Maiúsculas",
     ylab="Frequência",main="Letras Maiúsculas em spam (vermelho) e em ham (preto)", pch=19)
abline(h=2.9, lty=3, col="blue")

Então podemos criar o seguinte modelo:

• letras maiúsculas > 2.9 e entre 2.3 e 2.5 \(\Rightarrow\) spam
• letras maiúsculas < 2.3 e entre 2.5 e 2.9 \(\Rightarrow\) não spam

plot(spamMenor$capitalAve,col=spamRotulos,xlab="Quantidade de Letras Maiúsculas",
     ylab="Frequência",main="Letras Maiúsculas em spam (vermelho) e em ham (preto)", pch=19)
abline(h=c(2.9, 2.3, 2.5), lty=3, col="blue")

# construindo o modelo sobreajustado
modelo.sobreajustado=function(x){
  predicao=rep(NA,length(x))
  predicao[x>2.9]="spam"
  predicao[x<2.3]="nonspam"
  predicao[(x>=2.3 & x<=2.5)]="spam"
  predicao[(x>2.5 & x<=2.9)]="nonspam"
  return(predicao)
}
# avaliando o modelo sobreajustado
resultado=modelo.sobreajustado(spamMenor$capitalAve)
table(resultado,spamMenor$type)

Note que obtivemos uma precisão perfeita nessa amostra, como já era esperado. Nesse caso, o erro dentro da amostra é de 0%. Mas, será que esse modelo é o mais eficiente em outros dados também?

Vamos criar essa segunda regra para um modelo geral:

• letras maiúsculas > 2.9 \(\Rightarrow\) spam
• letras maiúsculas <= 2.9 \(\Rightarrow\) não spam

plot(spamMenor$capitalAve,col=spamRotulos,xlab="Quantidade de Letras Maiúsculas",
     ylab="Frequência",main="Letras Maiúsculas em spam (vermelho) e em ham (preto)", pch=19)
abline(h=2.8, lty=3, col="blue")
# construindo o modelo geral
modelo.geral=function(x){
  predicao=rep(NA,length(x))
  predicao[x>2.9]="spam"
  predicao[x<=2.9]="nonspam"
  return(predicao)
}
# avaliando o modelo geral
resultado2=modelo.geral(spamMenor$capitalAve)
table(resultado2,spamMenor$type)

Observe que dessa forma temos um erro dentro da amostra de 10%. Vamos agora aplicar esses dois modelos para toda a base de dados:

table(modelo.sobreajustado(spam$capitalAve),spam$type)
table(modelo.geral(spam$capitalAve),spam$type)

Olhando para a precisão de nossos modelos:

sum(modelo.sobreajustado(spam$capitalAve)==spam$type)
sum(modelo.geral(spam$capitalAve)==spam$type)

Observe que o erro fora da amostra no modelo sobreajustado foi de 27.10%, enquanto o erro do modelo geral foi de 26.06%. Note que se queremos construir um modelo que melhor representa qualquer amostra que pegarmos, um modelo não sobreajustado possui precisão maior.

---

Avaliando Preditores – Introdução ao Pacote Caret

O pacote caret (abreviação de Classification And Regression Training) é um pacote muito útil para o machine learning pois envolve algoritmos que possibilitam que as previsões sejam feitas de forma mais prática, simplificando o processo de criação de modelos preditivos. Nesse guia detalhado pode ser encontrado mais informações sobre o pacote.

Avaliando Classificadores {#link3}

Vamos utilizar a base de dados spam novamente para realizarmos o procedimento de predição para um e-mail (se ele é spam ou não spam), dessa vez utilizando o pacote caret.

Para fazer a separação da amostra em treino e teste vamos primeiramente particionar a base de dados com a função createDataPartition().

library(caret)
library(kernlab)
data(spam)
set.seed(371)
noTreino = createDataPartition(y = spam$type, p = 0.75, list = F)

Essa função retorna os números das linhas a serem selecionadas para o treino. Os principais argumentos são:

• y = classe dos dados que deverá ser mantida a mesma proporção nos conjuntos treino e teste. Para o nosso exemplo, escolhemos manter a mesma proporção do tipo do e-mail. Sendo assim, tanto no treino como no teste teremos a mesma proporção de e-mails spam e não spam.
• p = porcentagem da amostra que será utilizada para o treino. Para o nosso exemplo, escolhemos 75%.
• list = argumento do tipo logical, se TRUE \(\rightarrow\) os resultados serão mostrados em uma lista, se FALSE \(\rightarrow\) os resultados serão mostrados em uma matriz.

OBS: Esse comando deve ser utilizado apenas quando os dados são amostras independentes.

Agora vamos separar o que irá para o treino e o que irá para o teste.

# Separando as linhas para o treino:
treino = spam[noTreino,]
# Separando as linhas para o teste:
teste = spam[-noTreino,]

Dado que já foi feito a separação das amostras treino e teste, o próximo passo é realizarmos o treinamento. Para isso é preciso escolher um dos modelos para ser utilizado. Uma lista com todos os modelos implementados no pacote caret pode ser vista com o seguinte comando:

names(getModelInfo())

Para o nosso exemplo vamos utilizar o “glm” (generalized linear model).

Agora vamos criar o nosso modelo, utilizando apenas a amostra treino. Para isso vamos usar o comando train().

modelo = train(type ~ ., data = treino, method = "glm")

No primeiro argumento colocamos qual variável estamos tentando prever em função de qual(is). No nosso caso, queremos prever “type” em função (“~”) de todas as outras, por isso utilizamos o “.”. Em seguida dizemos de qual base de dados queremos construir o modelo e por último o método de treinamento utilizado.

Agora vamos dar uma olhada no nosso modelo.

modelo

Podemos observar que utilizamos uma amostra de tamanho 3451 no treino e 57 preditores para prever a qual classe um e-mail pertence, spam ou não spam. O que a função faz é realizar várias maneiras diferentes de testar se esse modelo funcionará bem e usar isso para selecionar o melhor modelo. Neste caso ela usou a reamostragem por bootstrapping com 25 replicações (o default da função).

Uma vez que ajustamos o modelo podemos aplicá-lo na amostra teste, para estimarmos a precisão do classificador. Para isso utilizamos o comando predict(). Dentro da função nós passamos o modelo que ajustamos no treino e em qual base de dados gostaríamos de realizar a predição.

predicao = predict(modelo, newdata = teste)
head(predicao, n=30)

Ao fazermos isso obtemos uma série de predições para as classes dos e-mails do conjunto teste. Podemos então realizar a avaliação do modelo comparando os resultados da predição com as reais classes dos e-mails, por meio do comando confusionMatrix().

Matriz de Confusão (Confusion Matrix) {#link2}

A matriz de confusão é a matriz de comparação feita após a predição, onde as linhas correspondem ao que foi previsto e as colunas correspondem à verdade conhecida.

Exemplo: A matriz de confusão para o problema de predição dos e-mails em spam ou não spam fica da seguinta forma:

Onde na primeira coluna se encontram os elementos que possuem a característica de interesse (os e-mails que são spam), e, respectivamente nas linhas, os que foram corretamente identificados – o qual são chamados de Verdadeiros Positivos (VP) – e os que foram erroneamente identificados – os Falsos Negativos (FP). Na segunda coluna se encontram os elementos que não possuem a característica de interesse (os e-mails que são ham) e, respectivamente nas linhas, os que foram erroneamente identificados – o qual são chamados de Falsos Positivos (FN) – e os que foram corretamente identificados – os Verdadeiros Negativos (VN).

Com as devidas classificações a matriz de confusão fica da seguinte forma:

Dentro da função passamos as predições que obtemos pelo modelo ajustado e as reais classificações dos e-mails do conjunto teste.

confusionMatrix(predicao, teste$type)

A função retorna a matriz de confusão e alguns dados estatísticos, como por exemplo a Precisão (Accuracy), o Intervalo de Confiança com 95% de confiança (95% CI), a Sensibilidade (Sensitivity), Especificidade (Specificity), entre outros.

Podemos notar que o GLM foi um bom modelo de treinamento para os nossos dados pois obtivemos altas taxas de acertos: uma precisão de 0,94, 0,96 de sensitividade e 0,90 de especificidade. Vamos ver melhor algumas dessas estatísticas:

Definição (Sensibilidade): A sensibilidade de um método de predição é a porcentagem dos elementos da amostra que possuem a característica de interesse e foram corretamente identificados. Para o nosso exemplo dos e-mails, a sensabilidade é a porcentagem dos e-mails que são spam e foram classificados pelo nosso algoritmo de predição como spam.

Ou seja, podemos escrever \[Sensibilidade = \frac{VP}{VP+FN}\]

Definição (Especificidade): A especificidade de um método de predição é a porcentagem dos elementos da amostra que não possuem a característica de interesse e foram corretamente identificados. Para o nosso exemplo dos e-mails, a especificidade é a porcentagem dos e-mails que são “ham” e o algoritmo de predição os classificou como tal.

Ou seja, podemos escrever \[Especificidade=\frac{VN}{VN+FP}\]

Quando obtemos as sensibilidades e as especificidades de diferentes preditores, naturalmente surge o questionamente: qual deles é melhor para estimar as verdadeiras características de interesse? A resposta depende do que é mais importante para o problema.

Se identificar corretamente os positivos for mais importante, utilizamos o preditor com maior sensibilidade. Se identificar corretamente os negativos for mais importante, utilizamos o preditor com maior especificidade.

Outra medida para avaliar a qualidade do nosso preditor é a precisão (Accuracy). Ela avalia a porcentagem de acertos que tivemos em geral. Ou seja, somamos o número de Verdadeiros Positivos com o número de Verdadeiros Negativos e dividimos pelo tamanho da amostra. \[Precisão=\frac{VP+VN}{VP+VN+FN+FP}\]

Para demais medidas da matriz de confusão consulte o apêndice.

Avaliando Regressores

Agora vamos utilizar a base de dados faithful para tentar prever o tempo em que o gêiser Old Faithful dos Estados Unidos permanece em erupção dado o tempo entre as erupções.

data("faithful")
head(faithful)

Primeiro, vamos separar a amostra em treino e teste.

set.seed(39)
noTreino = createDataPartition(y=faithful$eruptions, p=0.7, groups = 5, list=F)
treino = faithful[noTreino,]; teste = faithful[-noTreino,]

Quando o argumento y é numérico, a amostra é dividida em grupos com base nos percentis e é feita uma amostragem estratificada. o número de percentis é definido pelo argumento groups.

Agora temos que treinar nosso modelo. Para esse exemplo vamos usar a Regressão Linear (lm – Linear Regression).

Os métodos disponíveis e seus usos podem ser encontrados no guia do caret.

Vamos treinar nosso modelo utilizando a amostra treino.

modelo = caret::train(eruptions~waiting, data = treino, method = "lm")

Novamente, colocamos a variável que tentamos prever em função das outras. No caso, só temos duas variáveis então não precisamos colocar o ponto como no classificador.

modelo

Podemos ver que temos 192 observações no conjunto treino e 1 preditor.

Agora vamos aplicar nosso modelo na amostra teste para avaliar o erro dele.

predicao = predict(modelo, newdata = teste)

Assim como no classificador, a função predict nos retorna a previsão de tempo de erupção para cada observação na amostra teste dados o tempo entre as erupções. Podemos avaliar nosso erro de predição através do Erro Quadrático Médio.

MSE {#link1}

Assim como há diversas formas de compararmos a qualidade dos classificadores, há também diversas formas de compararmos regressores. O que estudaremos agora é o MSE (mean squared error – erro quadrático médio). Mais formas de comparação de regressores também serão vistas futuramente.

O MSE é a média de quanto os valores previstos para as observações se distanciaram dos valores verdadeiros dessa observação. Obtemos ele somando essas distâncias entre os valores previstos e os reais ao quadrado e dividindo por n.

\[MSE=\frac{1}{n} \sum\limits_{i=1}^{n} \left( Yreal_i-Yestimado_i \right)^{2}\]

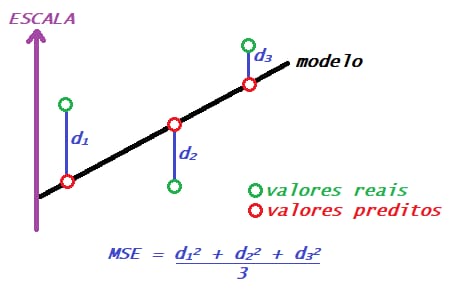
Ex.: O erro quadrático médio para o problema de tempo de erupção do gêiser.

data("faithful")
head(faithful)

# Gráfico do tempo de erupção do gêiser em função do tempo entre as erupções
plot(faithful$waiting, faithful$eruptions, pch = 20, xlab="Tempo entre erupções",
     ylab = "Tempo de erupção", main = "Tempo de erupção do gêiser em função do tempo entre as erupções")

Podemos notar que há uma relação linear positiva entre as variáveis. Vamos então ajustar um modelo de regressão linear.

modelo = lm(faithful$eruptions~faithful$waiting)
plot(faithful$waiting, faithful$eruptions, pch = 20, xlab="Tempo entre erupções",
     ylab = "Tempo de erupção", main = "Tempo de erupção do gêiser em função do tempo entre as erupções")
abline(modelo, col = "red", lwd = 2)

Na reta de regressão temos todos os valores previstos para o tempo de erupção de acordo com os tempos de espera. Podemos então calcular o MSE para o nosso modelo utilizando o comando mse().

mse = sum((teste$eruptions-predicao)**2)/length(teste)
mse

Então temos que, em média, o valor estimado para a variável de interesse no conjunto de teste se distancia do valor real observado em 8,91 escores. Note que esta é uma medida que soma as distâncias ao quadrado, por isso o MSE é um número relativamente grande.

---

Cross Validation (Validação Cruzada)

Existem diversos métodos de aprendizado de máquina que podemos usar para construir um preditor. Então como saber qual método é melhor? Um jeito de fazer isso é usando a validação cruzada.

A Validação Cruzada nos permite comparar diferentes métodos de aprendizado de máquina ou parâmetros para o método escolhido e avaliar qual funcionará melhor na prática.

Então o que vamos fazer é, para cada método,

1. Separar os dados em conjunto de treino e conjunto de teste.
2. Treinar um modelo no conjunto de treino.
3. Avaliar no conjunto de teste
4. Repetir os passos 1-3 e estimar o erro.

Bem, já sabemos que não é uma boa ideia usar toda a base de dados para treinar o nosso preditor e então podemos dividir por exemplo os primeiros 75% dos dados para treino e 25% finais para teste. Mas, e se esse não for o melhor jeito de dividir nossos dados? E se o melhor jeito de fazer essa divisão for usando os primeiros 25% para teste e o restante para treino? A Validação cruzada leva em consideração todas essas divisões usando uma de cada vez e tirando a média dos resultados no final. Para isso veremos como realizar alguns métodos de reamostragem, para utilizarmos várias amostras possíveis e não ficarmos dependentes de uma única amostra.

Alguns Métodos de Reamostragem

Agora vamos compreender como fatiar os dados para realizarmos a reamostragem. Existem vários métodos possíveis mas vamos nos focar em três: k-fold, repeated k-fold e bootstrap.

K-fold

Este método consiste em fatiar os dados em k pedaços iguais. Utilizamos um pedaço para o teste e os demais para o treino. Então realizamos esse procedimento k vezes, de modo que em cada repetição um novo pedaço seja utilizado para o teste. Para avaliar o erro nós tiramos a média de todos os erros de todas as replicações.

Exemplo: K-fold com 10 partes:

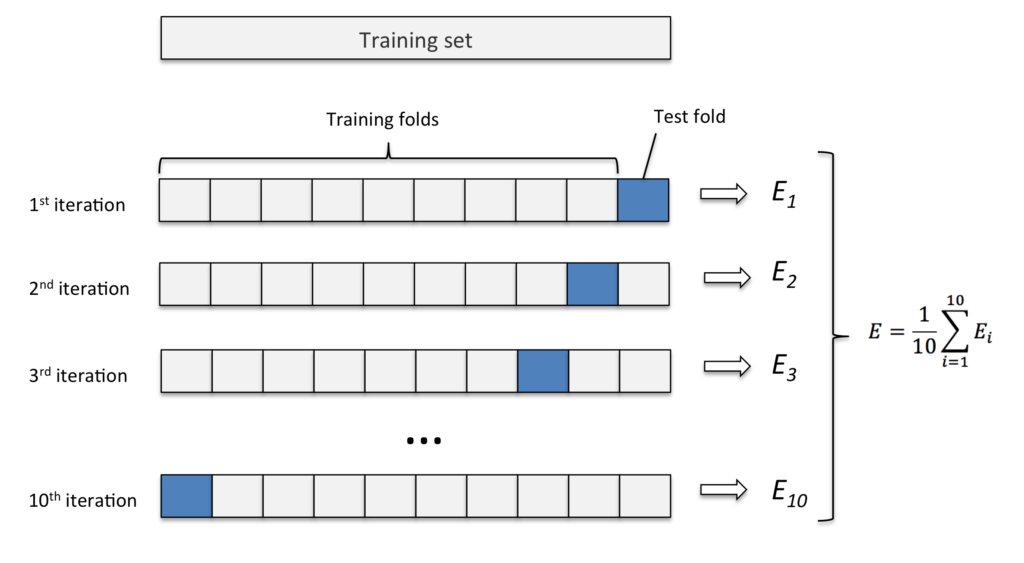
Quanto maior o k escolhido obtemos menos viés, porém mais variância. Em outras palavras, você terá uma estimativa muito precisa do viés entre os valores previstos e os valores verdadeiros, porém altamente variável. Agora quanto menor o k escolhido, mais viés e menos variância. Ou seja, não iremos necessariamente obter uma boa estimativa do viés, mas ela será menos variável.

OBS: Quando o k é igual ao tamanho da amostra, o método é também conhecido como leave-one-out.

Ex.: vamos utilizar reamostragem por k-fold no conjunto de dados spam.

library(caret)
library(kernlab)
data(spam)
noTreino = createDataPartition(y = spam$type, p = 0.75, list = F)
treino = spam[noTreino,]
teste = spam[-noTreino,]
# Para fazer a reamostragem por k-fold vamos utilizar o comando createFolds():
folds = createFolds(y = spam$type, k = 10, list = T, returnTrain = T)

Os principais argumentos da função createFolds() são:

• y = a variável de interesse (no nosso caso, o tipo do e-mail);
• k = o número (inteiro) de partições que você deseja.
• list = argumento do tipo logical. Se TRUE \(\rightarrow\) os resultados serão mostrados em uma lista, se FALSE \(\rightarrow\) os resultados serão mostrados em uma matriz.
• returnTrain = argumento do tipo logical. Se TRUE, retorna amostras treino. Se FALSE, retorna amostras teste.

Vamos verificar o tamanho de cada partição da nossa amostra treino:

sapply(folds,length)

Agora vamos fazer o mesmo para a amostra teste:

folds = createFolds(y = spam$type, k = 10, list = T, returnTrain = F)
sapply(folds,length)

Outra opção de realizar a reamostragem por k-fold é aplicá-la diretamente na função train.

controle = trainControl(method = "cv", number = 10)
modelo = caret::train(type ~ ., data = spam, method = "glm", trControl = controle)

Repeated K-fold

O repeated k-fold se resume a repetir o método k-fold várias vezes, com o objetivo de melhorar nossa reamostragem.

Ex.: Vamos aplicar um método de treino 3 vezes em 10 folds.

controle = trainControl(method = "repeatedcv", number = 10, repeats = 3)
modelo = caret::train(type ~ ., data = spam, method = "glm", trControl = controle)

Bootstrap {#link5}

O bootstrap é uma técnica de reamostragem com o propósito de reduzir desvios e realizar amostragem dos dados de treino com repetições. Já vimos anteriormente que este é o método default do comando train(), onde é feito 25 reamostragens por bootstrap.

Embora esse seja o padrão podemos alterar através do comando trainControl(). Por exemplo, vamos alterar o número de reamostragens de 25 para 10.

controle = trainControl(method = "boot", number = 10)
modelo = train(type ~ ., data = spam, method = "glm", trControl = controle)

Podemos também realizarmos bootstrap fora da função train(), utilizando o comando createResample().

folds = createResample(y = spam$type, times = 10, list = F)

---

Comparando Funções Preditoras

Como já foi dito em capítulos anteriores, existem diversas formas de comparar preditores. Nesse capítulo, vamos estudar um meio de fazer isso e ver mais detalhadamente as medidas de comparação que o R retorna ao usarmos esse método.

Exemplo de Comparação de Regressores – base faithful

Vamos usar a base de dados faithful já presente no R.

data("faithful")
# verificando a estrutura da base
str(faithful)

Note que a base apresenta apenas duas variáveis: eruptions, que contém uma amostra corresponde ao tempo em minutos que o gêiser Old Faithful permanece em erupção e waiting, que contém uma amostra correspondente ao tempo em minutos até a próxima erupção. Vamos tentar prever a variável eruptions através da variável waiting. Note ainda que a variável de interesse é quantitativa contínua, portanto queremos construir um Regressor.

Vamos treinar nosso modelo utilizando 3 métodos separadamente: linear model, Projection Pursuit Regression e k-Nearest Neighbour. Para fazer a comparação, vamos colocar a mesma semente antes de cada treino para que todos sejam feitos da mesma forma e assim torne a comparação mais “justa”. Note também que estamos usando toda a base de dados pra treinar o medelo. Isso porque estamos apenas avaliando o melhor modelo.

library(caret)
# usando o método de validação cruzada, tiramos a dependecia da amostra
TC = trainControl(method="repeatedcv", number=10,repeats=3)
set.seed(371)
modelo_lm = train(eruptions~waiting, data=faithful, method="lm", trControl=TC)
set.seed(371)
modelo_ppr = train(eruptions~waiting, data=faithful, method="ppr", trControl=TC)
set.seed(371)
modelo_knn = train(eruptions~waiting, data=faithful, method="knn", trControl=TC)

Agora, como sabemos qual desses é o melhor modelo para nosso Regressor?

resultados = resamples(list(LM=modelo_lm, PPR=modelo_ppr, KNN=modelo_knn))
summary(resultados)

Repare que foi calculada três diferentes medidas: “MAE”, “RMSE”, e “Rsquared”.

O Erro Médio Absoluto (MAE – Mean Absolute Error) é dado pelo média dos desvios absolutos. \[MAE = \frac{\sum\limits_{i=1}^{n}\mid estimado_i – real_i\mid}{n}\quad, i=1,2,…,n.\]

A Raiz do Erro Quadrático Médio (RMSE – Root Mean Squared Error), como o nome já diz, não é nada mais que a raiz quadrada do Erro Quadrático Médio já citado no capítulo de Tipos de Erro. \[RMSE=\sqrt{MSE}=\sqrt{\frac{\sum\limits_{i=1}^{n} \left( estimado_i-real_i \right)^{2}}{n}}\quad, i=1,2,…,n.\]

O Coeficiente de Determinação, Também chamado de \(R^2\) (R squared), é dado pela razão entre o MSE e a Variância subtraído de 1. \[R^2 =1- \frac{MSE}{Var}= 1-\frac{\sum\limits_{i=1}^{n} (real_i – estimado_i)^2}{\sum\limits_{i=1}^{n} (real_i – média)^2}\quad, i=1,2,…,n.\]

Portanto, queremos o modelo que possua MAE e RMSE baixo e \(R^2\) alto. Para vizualizar melhor, podemos construir um boxplot comparativo da seguinte forma

# ajustando as escalas dos graficos
escala <- list(x=list(relation="free"), y=list(relation="free"))
# plotando os dados
bwplot(resultados, scales=escala)

Pelos boxplots parece que o modelo linear é o que possui a pior mediana nas três medidas comparativas e parece ter os dados mais espalhados, principalmente no \(R^2\), o que indica que ele possui alta variabilidade. Quanto ao KNN e o PPR, os dados estão mais concentrados no RMSE \(R^2\) embora tenha bastante outliers. Parece que o PPR é levemente melhor que o KNN, mas é preciso uma análise mais profunda.

library(lattice)
# Comparando o comportamento de cada fold nos modelos KNN e PPR
xyplot(resultados, models=c("PPR", "KNN"))

Note que a maior parte dos folds está abaixo da diagonal, indicando que o PPR tem um erro absoluto médio (MAE) menor que o KNN. Vamos olhar novamente para o calculo que fizemos mais acima.

resultados = resamples(list(LM=modelo_lm, PPR=modelo_ppr, KNN=modelo_knn))
summary(resultados)

Podemos notar que o PPR tem uma posição melhor que o KNN em todas as medidas. Como saber se essa diferença é significativa? Vamos calcular as diferenças entre os dois modelos e avaliar por p-valor.

#Calcular diferença entre modelos, e realizar
#testes de hipótese para as diferenças.
diferencas = diff(resultados)
summary(diferencas)

Observe que, para cada medida, acima da diagonal temos a diferença entre os modelos e abaixo da diagonal o p-valor do teste de comparação entre eles. Portanto, se considerarmos um nível de significância de 1%, é razoável dizer que os modelos PPR e KKN produzem resultados significativamente diferentes. Sendo assim, escolheriamos o método PPR para treinar nosso modelo.

Exemplo de Comparação de Classificadores – base Heart {#link6}

Suponha agora que queremos predizer se uma pessoa tem ou problema no coração dado que ela apresentou dor no peito. Considere a seguinte base de dados.

library(readr)
# lendo a base de dados
heart = read_csv("Heart.csv")
# verificando a estrutura da base
str(heart)

Note que a variável de interesse HeartDisease é categórica, portanto estamos trabalhando com um Classificador.

Vamos treinar nosso modelo utilizando 3 métodos separadamente: Recursive Partitioning and Regression Trees, Fitting Generalized Linear Models e Support Vector Machines. Novamente, vamos colocar a mesma semente antes de cada treino e utilizar toda a base de dados pra isso.

library(caret)
# usando o método de validação cruzada tiramos a dependência da amostra
TC = trainControl(method="repeatedcv", number=10,repeats=3)
set.seed(371)
modelo_rpart = caret::train(HeartDisease~., data=heart, method="rpart", trControl=TC)
set.seed(371)
modelo_glm = caret::train(HeartDisease~., data=heart, method="glm", trControl=TC)
set.seed(371)
modelo_svm = caret::train(HeartDisease~., data=heart, method="svmLinear", trControl=TC)

Assim como no caso anterior, vamos comparar os resultados obtidos por cada modelo.

resultados = resamples(list(Rpart=modelo_rpart, GLM=modelo_glm, SVM=modelo_svm))
summary(resultados)

Repare que foi calculada duas diferentes medidas: “Accuracy”, e “Kappa”.

A Precisão (Accuracy) como já foi citado no capítulo Introdução ao pacote caret, avalia a proporção de acertos na predição.\[Precisão=\frac{Predições\ corretas}{Total\ de\ predições}\]

O Coeficiente de concordância Kappa avalia o grau de concordância entre a classificação e o real valor de uma mesma amostra. E é calculado da seguinte forma:

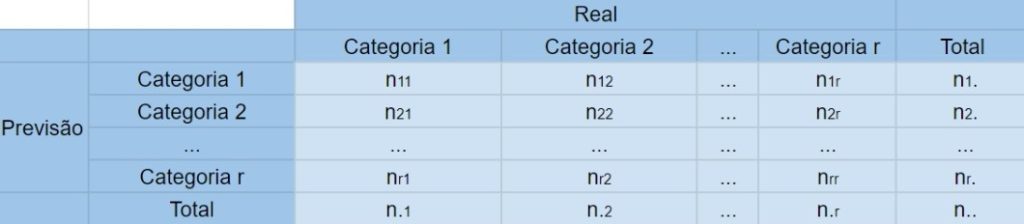
\[\hat{K}=\frac{\hat{p_0}-\hat{p_e}}{1-\hat{p_e}},\quad \hat{p_0}=\sum^{r}_{i}\frac{n_{ii}}{n} \quad e \quad\hat{p_e}=\sum^{r}_{i}\frac{n_{i.}*n_{.i}}{n^2}\]

Portanto, queremos que as duas medidas sejam altas. Vamos ver o boxplot.

# ajustando as escalas dos graficos
escala <- list(x=list(relation="free"), y=list(relation="free"))
# plotando os dados
bwplot(resultados, scales=escala)

Pelo boxplot podemos ver que o método Rpart possui uma alta variabilidade. O método GLM está com uma mediana melhor e parece mais concentrado. Mas será que ele é mesmo melhor que o SVM?

# Comparando o comportamento de cada fold nos modelos KNN e PPR
xyplot(resultados, models=c("GLM", "SVM"))

Por esse plot, não parece haver uma diferença significativa entre os dois métodos. Vamos voltar a nossas medidas.

resultados = resamples(list(Rpart=modelo_rpart, GLM=modelo_glm, SVM=modelo_svm))
summary(resultados)

A precisão e kappa média também parecem próximas entre o GLM e o SVM. Vamos fazer então um teste de hipótese para confirmar.

#Calcular diferença entre modelos, e realizar
#testes de hipótese para as diferenças.
diferencas = diff(resultados)
summary(diferencas)

Note que o p-valor da diferença é 1. Portanto, concluímos que não existe uma diferença significativa entre os métodos GLM e SVM para este caso.

Mas, e quanto ao tempo de processamento de cada modelo? Vamos usar a função Sys.time() para medir o tempo de treinamento nos dois métodos.

inicio1 <- Sys.time()
set.seed(371)
modelo_glm = train(HeartDisease~., data=heart, method="glm", trControl=TC)
fim1 <- Sys.time()
fim1 - inicio1

inicio2 <- Sys.time()
set.seed(371)
modelo_svm = train(HeartDisease~., data=heart, method="svmLinear", trControl=TC)
fim2 <- Sys.time()
fim2 - inicio2

Bem, não parece que a diferença foi muito grande. Mas, pense agora que você quer realizar uma comparação usando a validação cruzada com 20 folds e 100 repetições.

TC = trainControl(method="repeatedcv", number=20,repeats=100)

inicio1 <- Sys.time()
set.seed(371)
modelo_glm = train(HeartDisease~., data=heart, method="glm", trControl=TC)
fim1 <- Sys.time()
fim1 - inicio1

inicio2 <- Sys.time()
set.seed(371)
modelo_svm = train(HeartDisease~., data=heart, method="svmLinear", trControl=TC)
fim2 <- Sys.time()
fim2 - inicio2

A diferença de processamento agora já é um pouco maior. Mas, lembre que nossa base de dados contém apenas 297 observações e 15 variáveis. Numa base de dados muito grande e/ou em determinados métodos esse tempo fará diferença.

---

Pré-Processamento

Antes de criarmos um modelo de predição, é importante plotarmos as variáveis do nosso modelo antecipadamente para observarmos se há algum comportamento estranho entre elas. Por exemplo, podemos ter uma variável que assuma frequentemente um único valor (possui muito pouca variabilidade), o que não acrescenta informações relevantes ao modelo, ou uma que possua alguns dados faltantes (NA’s). O que podemos fazer nesses casos, que é o que iremos estudar neste capítulo, é realizar alterações em tais variáveis, afim de melhorar/otimizar a nossa predição/classificação. Essa é a ideia de pré-processar.

Padronizando os Dados

Vamos carregar o banco de dados spam e criar amostras treino e teste.

library(kernlab)
library(caret)
data(spam)
set.seed(123)
noTreino = createDataPartition(y = spam$type, p = 0.75, list = F)
treino = spam[noTreino,]
teste = spam[-noTreino,]
# Vamos olhar para a variável capitalAve (média de letras maiúsculas por linha):
hist(treino$capitalAve,
     ylab = "Frequência",
     xlab = "Média de Letras Maiúsculas por Linha",
     main = "Histograma da Média de Letras Maiúsculas por Linha",
     col="steelblue", breaks = 4)

Podemos notar que muitos elementos estão próximos do 0 e os outros estão muito espalhados. Ou seja, essa variável não está trazendo muita informação para o modelo.

mean(treino$capitalAve)

sd(treino$capitalAve)

Podemos ver que a média é pequena mas o desvio padrão é muito grande.

Para que os algoritmos de machine learning não sejam enganados pelo fato de a variável ser altamente variável, vamos realizar um pré-processamento. Vamos padronizar os dados da variável pela amostra treino pegando cada valor dela e subtraindo pela sua média e dividindo pelo seu desvio padrão.

treinoCapAve = treino$capitalAve
# Padronizando a variável:
treinoCapAveP = (treino$capitalAve-mean(treinoCapAve))/sd(treinoCapAve)
# Média da variável padronizada:
mean(treinoCapAveP)

Agora temos média 0.

# Desvio padrão da variável padronizada:
sd(treinoCapAveP)

E variância 1.

# Vamos olhar para a variável capitalAve (média de letras maiúsculas por linha):
hist(treinoCapAveP, ylab = "Frequência", xlab = "Média de Letras Maiúsculas por Linha",
     main = "Histograma da Média de Letras Maiúsculas por Linha",col="steelblue", breaks =4)

Agora vamos aplicar a mesma transformação na amostra teste. Uma coisa a ter em mente é que ao aplicar um algoritmo no conjunto de teste, só podemos usar os parâmetros que estimamos no conjunto de treino. Ou seja, temos que usar a média e o desvio padrão da variável capitalAve do TREINO.

testeCapAve = teste$capitalAve
# Aplicando a transformação:
testeCapAveP = (testeCapAve-mean(treinoCapAve))/sd(treinoCapAve)
# Média da variável transformada do conjunto teste:
mean(testeCapAveP)

# Desvio Padrão da variável transformada do conjunto teste:
sd(testeCapAveP)

Nesse caso não obtemos média 0 e variância 1, afinal nós utilizamos os parâmetros do treino para a padronização. Mas podemos notar que os valores estão relativamente próximos disso.

Padronizando os Dados com a Função preProcess()

Podemos realizar o pré-processamento utilizando a função preProcess() do caret. Ela realiza vários tipos de padronizações, mas para utilizarmos a mesma (subtrair a média e dividir pelo desvio padrão) utilizamos o método c(“center”,“scale”).

padronizacao = preProcess(treino, method = c("center","scale"))
# O comando acima cria um modelo de padronização. Para ter efeito ele deve ser aplicado nos dados com o
# comando predict().
treinoCapAveS = predict(padronizacao,treino)$capitalAve
# Média da variável padronizada:
mean(treinoCapAveS)

# Desvio padrão da variável padronizada:
sd(treinoCapAveS)

Note que chegamos à mesma média e variância de quando padronizamos sem o preProcess().

Agora vamos aplicar essa padronização no conjunto de teste:

testeCapAveS = predict(padronizacao,teste)$capitalAve
# Note que aplicamos o modelo de padronização criado com a amostra treino.

Observe que também encontramos o mesmo valor da média e desvio padrão de quando padronizamos a variável do conjunto teste anteriormente (sem o preProcess()):

mean(testeCapAveS)

sd(testeCapAveS)

Repare que também chegamos à mesma média e variância de quando padronizamos sem o preProcess().

preProcess como argumento da função train()

Também podemos utilizar o preProcess dentro da função train da seguinte forma:

modelo = train(type~., data = treino, preProcess = c("center","scale"), 
               method = "glm")

A única limitação é que esse método aplica a padronização em todas as variáveis numéricas.

Obs.: Quando for padronizar uma variável da sua base para depois treinar seu algoritmo, lembre-se que colocar a variável padronizada de volta na sua base.

Tratando NA’s

É muito comum encontrar alguns dados faltantes (NA’s) em uma base de dados. E quando você usa essa base para fazer predições, o algoritmo preditor muitas vezes falha, pois eles são criados para não manipular dados ausentes (na maioria dos casos). O mais recomendado a se fazer é descartar esses dados, principalmente se o número de variáveis for muito pequeno. Porém, em alguns casos, podemos tentar substituir os NA’s da amostra por dados de outros elementos que possuam características parecidas.

Obs: Este é um procedimento que deve ser feito com muito cuidado, apenas em situações de real necessidade.

Método k-Nearest Neighbors (knn)

O método k-Nearest Neighbors (knn) consiste em procurar os k vizinhos mais próximos do elemento que possui o dado faltante de uma variável de interesse, calculando a média dos valores observados dessa variável dos k vizinhos e imputando esse valor ao elemento.

Vamos utilizar novamente a variável capitalAve do banco de dados spam como exemplo.

library(kernlab)
library(caret)
data(spam)
set.seed(13343)
# Criando amostras treino e teste:
noTreino = createDataPartition(y = spam$type, p = 0.75, list = F)
treino = spam[noTreino,]
teste = spam[-noTreino,]

Originalmente, a variável capitalAve não possui NA’s. Mas para o objetivo de compreendermos como esse método funciona, vamos inserir alguns valores NA’s.

NAs = rbinom(dim(treino)[1], size = 1, p = 0.05)==1

O que fizemos com a função rbinom() é criar uma amostra de tamanho “dim(treino)[1]” (quantidade de elementos no treino) de uma variável Bernoulli com probabilidade de sucesso = 0,05. Ou seja, o vetor NAs será um vetor do tipo logical, onde será TRUE se o elemento gerado pela rbinom() é “1” (probabilidade de 0,05 de acontecer) e FALSE se é “0” (probabilidade 0,95 de acontecer).

Para preservar os valores originais, vamos criar uma nova coluna de dados no treino chamada capAve, que será uma réplica da variável capitalAve, mas com os NA’s inseridos em alguns valores.

library(dplyr)

# Criando a nova variável capAve com os mesmos valores da capitalAve:
treino = treino %>% mutate(capAve = capitalAve)

# Inserindo os Na's:
treino$capAve[NAs] = NA 

Agora podemos aplicar o método KNN para imputar valores aos NA’s, escolhendo essa opção por meio do argumento “method” da função preProcess(). O padrão da função é utilizar k=5.

imput = preProcess(treino, method = "knnImpute")

# Aplicando o modelo de pré-processamento ao banco de dados treino:
treino$capAve = predict(imput,treino)$capAve

# Olhando para a variável capAve após o pré-processamento:
head(treino$capAve, n = 20)

Note que além de ter imputado valores aos NA’s, o comando knnImpute também padronizou os dados.

OBS: O método knnImpute só resolve os NA’s quando os dados faltantes são NUMÉRICOS.

E se quiséssemos aplicar o método de imputar valores aos NA’s em todo o conjunto de dados, e não só em apenas 1 variável? Também podemos fazer isso utilizando a função preProcess().

Vamos utilizar a base de dados “airquality”, já disponível no R, como exemplo.

base = airquality
head(base, n = 15)

Note que essa base possui alguns valores NA’s em algumas variáveis.

# Realizando o método KNN para imputar valores aos NA's:
imput = preProcess(base, method = "knnImpute")

# Aplicando o modelo em toda a base de dados:
nova_base = predict(imput, base)

# Vamos olhar para a nova base:
head(nova_base, n = 15)

Note que ela não possui mais NA’s e todas as variáveis foram padronizadas.

Utilizando Algoritmos de Machine Learning com o Pacote mlr

O pacote mlr fornece vários métodos de imputação para dados faltantes. Alguns desses métodos possuem técnicas padrões como, por exemplo, imputação por uma constante (uma constante fixa, a média, a mediana ou a moda) ou números aleatórios (da distribuição empírica dos dados em consideração ou de uma determinada família de distribuições). Para mais informações sobre como utilizar essas imputações padrões, consulte https://mlr.mlr-org.com/reference/imputations.html.

Entretanto, a principal vantagem desse pacote – que é o que abordaremos nessa seção – é a possibilidade de imputação dos valores faltantes de uma variável por meio de predições de um algoritmo de machine learning, utilizando como base as outras variáveis. Ou seja, além de aceitar valores faltantes de variáveis numéricas para a imputação, ele também aceita de variáveis categóricas.

Podemos observar todos os algoritmos de machine learning possíveis de serem utilizados nesse pacote através da função listLearners().

• Para um problema de imputação de NA’s de variáveis numéricas temos os seguintes métodos:

library(mlr)
knitr::kable(listLearners("regr", properties = "missings")["class"])

• Para um problema de imputação de NA’s de variáveis categóricas temos os seguintes métodos:

knitr::kable(listLearners("classif", properties = "missings")["class"])

Vamos utilizar o banco de dados “heart” para realizarmos a imputação de dados faltantes categóricos.

library(caret)
library(readr)
library(dplyr)

heart = read_csv("Heart.csv")

# Verificando se a base "heart" possui valores NA's em alguma variável:
apply(heart, 2, function(x) any(is.na(x)))

Note que a base não possui dados faltantes. Para fins didáticos, vamos inserir alguns na variável “Thal”.

# Criando um novo banco de dados que possuirá NA's:
new.heart = as.data.frame(heart)

set.seed(133)
# Criando um vetor do tipo *logical*, onde será TRUE se o elemento gerado pela rbinom() é "1"
# (probabilidade de 0,1 de acontecer):
NAs = rbinom(dim(new.heart)[1], size = 1, p = 0.1)==1

# Inserindo os NA's na variável Thal:
new.heart$Thal[NAs] = NA 
new.heart$Thal

Agora vamos imputar categorias aos dados faltantes da variável Thal. Iremos fazer isso através da função impute(). O único problema é que possuímos variáveis do tipo character na base de dados, e a função não aceita esta classe nos dados.

str(new.heart)

Vamos transformar essas categorias em fatores.

new.heart = mutate_if(new.heart, is.character, as.factor)

Vamos separar os dados em treino e teste.

set.seed(133)
noTreino = caret::createDataPartition(y = new.heart$HeartDisease, p = 0.75,
                                      list = F)
treino = new.heart[noTreino,]
teste = new.heart[-noTreino,]

treino=as.data.frame(treino)
teste=as.data.frame(teste)

Agora vamos imputar os dados no conjunto treino com a função impute().

Para isso passamos como argumento:

1. A base de dados que possui os valores faltantes;
2. A variável resposta do modelo, ou seja, a variável de interesse para predição. No nosso exemplo essa variável é a “HeartDisease”, que indica se uma pessoa possui uma doença cardíaca;
3. Lista contendo o método de imputação para cada coluna do banco de dados. Como apenas temos NA’s na variável “Thal”, a lista só possuirá essa variável, seguida do método de imputação que desejamos para ela. Vamos utilizar o método de árvores de decisão (“rpart”).

treino = mlr::impute(treino, target = "HeartDisease",
                     cols = list(Thal = imputeLearner("classif.rpart")))

Essa função retorna uma lista de tamanho 2, onde primeiro se encontra a base de dados após a imputação dos valores e em seguida detalhes do método utilizado.

Vamos olhar para a variável após a imputação dos dados:

treino$data[,"Thal"]

Para implementarmos esse algoritmo no conjunto de dados teste basta utilizarmos a função reimpute() que implementaremos o mesmo método com os mesmos critérios criados no conjuno treino. Basta passar os seguintes argumentos:

1. A base de dados que possui os valores faltantes;
2. O mesmo método utilizado no treino.

A função retorna a base de dados com os valores imputados.

teste = reimpute(teste, treino$desc)
teste$Thal

Variável Dummy

As variáveis dummies ou variáveis indicadoras são formas de agregar informações qualitativas em modelos estatísticos. Ela atribui 1 se o elemento possui determinada característica, ou 0 caso ele não possua. Esse tipo de transformação é importante para modelos de regressão pois ela torna possível trabalhar com variáveis qualitativas.

Vamos utilizar o banco de dados Wage, do pacote ISLR. Este banco possui informações sobre 3000 trabalhadores do sexo masculino de uma região dos EUA, como por exemplo idade (age), tipo de trabalho (jobclass), salário (wage), entre outras. Nosso objetivo é tentar prever o salário do indivíduo em função das outras variáveis.

library(ISLR)
data(Wage)
head(Wage)

Vamos olhar para 2 variáveis: jobclass (tipo de trabalho) e health_ins (indica se o trabalhador possui plano de saúde).

library(ggplot2)
Wage %>% ggplot(aes(x=jobclass)) + geom_bar(aes(fill=jobclass)) +
  ylab("Frequência") + guides(fill=F) + theme_light() +
  ggtitle("Gráfico de Barras para o Tipo de Trabalho")

Wage %>% ggplot(aes(x=health_ins)) + geom_bar(aes(fill=health_ins)) +
  ylab("Frequência") + guides(fill=F) + theme_light() +
  ggtitle("Gráfico de Barras para o Plano de Saúde")

Vamos transformar essas 2 variáveis em dummies por meio da função dummyVars().

dummies = dummyVars(wage~jobclass+health_ins, data = Wage)

# Aplicando ao modelo:
Dummies = predict(dummies, newdata = Wage)

head(Dummies)

Note que ele transforma cada categoria numa variável dummy. Ou seja, como temos 2 categorias para jobclass, cada uma delas vira uma variável dummy. Então se para um indivíduo temos um “1” na categoria “jobclass=industrial”, isso implica que terá um “0” na categoria “jobclass=information”, pois ou o indivíduo tem um tipo de trabalho, ou tem outro. O mesmo vale para as categorias de plano de saúde.

Observe também que esse novo modelo criado é uma matriz:

class(Dummies)

Vamos anexar esse novo objeto aos dados:

Wage_dummy = cbind(Wage, Dummies)
head(Wage_dummy)

# Removendo as variáveis categóricas do banco de dados completo (opcional):
Wage_dummy = dplyr::select(Wage_dummy, -c(jobclass,health_ins))
head(Wage_dummy)

Como comentado acima, nós temos uma variável dummy para cada categoria. Como tínhamos 2 variáveis qualitativas, então ficamos com 4 variáveis dummies. Porém, para um modelo de regressão, isso não é necessário. Estaríamos inserindo 2 variáveis com colinearidade perfeita no modelo: jobclass=industrial é totalmente correlacionada com jobclass=information, pois o resultado de uma influencia totalmente o da outra (o mesmo vale para as variáveis do plano de saúde). Dessa forma, vamos remover essas variáveis desnecessárias.

Wage_dummy = dplyr::select(Wage_dummy, -c("jobclass.2. Information","health_ins.2. No"))
head(Wage_dummy)

Uma maneira mais simples de fazer isso, sem precisarmos retirar cada variável “na mão”, é utilizar o argumento “fullRank=T” da função dummyVars().

dummies = dummyVars(wage~jobclass+health_ins, data = Wage, fullRank = T)

# Aplicando ao modelo:
Dummies = predict(dummies, newdata = Wage)

Note que o comando fullRank=T removeu a primeira variável de cada classificação.

# Anexando esse novo objeto aos dados:
Wage_dummy = cbind(Wage, Dummies)
head(Wage_dummy)

Variância Zero ou Quase-Zero {#link7}

Algumas vezes em um conjunto de dados podemos ter uma variável que assuma somente um único valor para todos os indivíduos, ou seja, ela possui variância zero. Ou podemos ter uma com uma frequência muito alta de um único valor, possuindo, assim, variância quase zero. Essas variáveis não auxiliam na predição, pois possuem o mesmo valor em muitos indivíduos, trazendo, assim, pouca informação ao modelo. Nosso objetivo é, então, identificar essas variáveis, chamadas de near zero covariates, para que possamos removê-las do nosso modelo de predição.

Para detectar as near zero covariates, utilizamos a função nearZeroVar() do pacote caret. Vamos verificar se há near zero covariates no banco de dados “forestfires”.

Na função nearZeroVar() passamos primeiro a base de dados a ser analisada, depois o argumento lógico “saveMetrics”, o qual se for “TRUE” retorna todos os detalhes sobre as variáveis da base de dados afim de identificar as near zero covariates. A saída da função fica da seguinte forma:

library(readr)
library(caret)
incendio = read_csv("forestfires.csv")
nearZeroVar(incendio, saveMetrics = T)

Note que é retornado uma tabela onde nas linhas se encontram as variáveis da base de dados e as colunas podemos resumir da seguinte forma:

• 1ª coluna: a Taxa de Frequência de cada variável. Essa taxa é calculada pela razão de frequências do valor mais comum sobre o segundo valor mais comum.
• 2ª coluna: a Porcentagem de Valores Únicos. Ela é calculada utilizando o número de valores distintos sobre o número de amostras.
• 3ª coluna: indica se a variável tem variância zero.
• 4ª coluna: indica se a variável tem variância quase zero.

Podemos observar que a variável “rain” possui variância quase zero, portanto ela é uma near zero covariate.

hist(incendio$rain, main = "Histograma da Variável Rain",
     xlab = "Variável Rain", ylab = "Frequência", col = "purple")

Logo, vamos excluir ela da nossa base de dados. O argumento “saveMetrics=FALSE” (default da função) retorna justamente qual(is) variável(is) do bando de dados é(são) near zero covariate .

nzv = nearZeroVar(incendio)
Nova_incendio = incendio[,-nzv]
head(Nova_incendio)

Análise de Componentes Principais (PCA)

Muitas vezes podemos ter variáveis em excesso no nosso banco de dados, o que torna difícil a manipulação das mesmas. A ideia geral do PCA (Principal Components Analysis) é reduzir a quantidade de variáveis, obtendo combinações interpretáveis delas. O PCA faz isso tranformando um conjunto de observações de variáveis possivelmente correlacionadas num conjunto de valores de variáveis linearmente não correlacionadas, chamadas de componentes principais. O número de componentes principais é sempre menor ou igual ao número de variáveis originais, e eles são selecionados de forma que expliquem uma alta porcentagem da variância do modelo.

Para utilizarmos o PCA no nosso modelo, basta colocar o argumento preProcess=“pca” na função train(). Por padrão, são selecionadas componentes que expliquem 95% da variância.

Vamos aplicar o método “glm”, com a opção “pca”, no banco de dados spam.

library(caret)
library(kernlab)
data(spam)
# Criando amostras treino/teste.
set.seed(36)
noTreino = createDataPartition(spam$type, p=0.75, list=F)
treino = spam[noTreino,] 
teste = spam[-noTreino,]

Agora vamos treinar o nosso modelo com o PCA.

set.seed(887)
modelo = caret::train(type ~ ., method = "glm", preProcess = "pca", data = treino)

# Aplicando o modelo na amostra TESTE:
testePCA = predict(modelo, teste)

Avaliando nosso modelo com a matriz de confusão:

confusionMatrix(teste$type, testePCA)

O modelo obteve uma acurácia de 0,93, o que pode-se considerar uma alta taxa de acerto.

É possível alterar a porcentagem de variância a ser explicada pelos componentes nas opções do train().

Por exemplo, vamos alterar a porcentagem da variância para 60%.

controle = trainControl(preProcOptions = list(thresh = 0.6))

# Treinando o modelo 2:
set.seed(754)
modelo2 = caret::train(type ~ ., method = "glm", preProcess = "pca", data = treino, trControl = controle)

# Aplicando o modelo 2:
testePCA2 = predict(modelo2, teste)

Avaliando o segundo modelo pela matriz de confusão:

confusionMatrix(teste$type,testePCA2)

Obtemos uma acurácia de 0,92, o que indica também uma alta taxa de acerto, porém um pouco menor que a do modelo anterior. Note que a sensitividade e a especificidade também diminuíram.

Em geral, são utilizados pontos de corte para a variãncia explicada acima de 0,9.

PCA fora da função train()

Podemos também realizar o pré-processamento fora da função train(). Primeiramente vamos criar o pré-processamento, utilizando a amostra treino.

PCA = preProcess(treino, method = c("center","scale","pca"), thresh = 0.95)

Obs: pode-se fixar o número de componentes, utilizando o argumento “pcaComp” ao invés de “thresh”.

Agora aplicamos o pré-processamento na amostra treino e realizamos o treinamento, utilizando a amostra treino já pré-processada.

treinoPCA = predict(PCA, treino)
modelo = caret::train(type ~ ., data = treinoPCA, method="glm")

Aplicando o pré-processamento na amostra teste:

testePCA = predict(PCA, teste)

Por último, aplicamos o modelo criado com a amostra treino na amostra teste pré-processada.

testeMod = predict(modelo, testePCA)

# Avaliando o modelo:
confusionMatrix(testePCA$type, testeMod)

Normalização dos Dados

Transformação de Box-Cox

A transformação de Box-Cox é uma transformação feita nos dados (contínuos) para tentar normalizá-los. Considerando \(X_1,…,X_n\) as variáveis do conjunto de dados original, essa transformação consiste em encontrar um \(\lambda\) tal que as variáveis transformadas \(Y_1,…Y_n\) se aproximem de uma distribuição normal com variância constante.

Essa transformação é dada pela seguinte forma: \[Y_i(\lambda)=\frac{X_i^{\lambda}-1}{\lambda} \hbox{ , se } \lambda \neq 0.\] O parâmetro \(\lambda\) é estimado utilizando o método de máxima verossimilhança.

O método de Box-Cox é o método mais simples e o mais eficiente computacionalmente. Podemos aplicar a transformação de Box-Cox nos dados através da função preProcess().

OBS: a transformação de Box-Cox só pode ser utilizada com dados positivos.

treinoBC = preProcess(treino, method = "BoxCox") 

Outras Transformações

Transformação de Yeo-Johnson

A transformação de Yeo-Johnson é semelhante à transformação de Box-Cox, porém ela aceita preditores com dados nulos e/ou dados negativos. Também podemos aplicá-la aos dados através da função preProcess().

treinoYJ = preProcess(treino, method = "YeoJohnson")

Transformação Exponencial de Manly

O método exponencial de Manly também consiste em estimar um \(\lambda\) tal que as variáveis transformadas se aproximem de uma distribuição normal. Assim como a transformação de Yeo-Johnson, ela também aceita dados positivos, nulos e negativos. Essa transformação é dada pela seguinte forma: \[Y_i(\lambda)=\frac{e^{X\lambda}-1}{\lambda} \hbox{ , se } \lambda \neq 0.\]

treinoEXP = preProcess(treino, method = "expoTrans")

---

Métodos de Treino Baseados em Árvores

Neste capítulo será estudado de forma mais aprofundada modelos de treinamento baseados em árvores, os quais são simples para interpretação, como: árvores de decisão e regressão, florestas aleatórias, adaboost, entre outros. O objetivo é entender o funcionamento dos mesmos, assim como os critérios que utilizam para classificarem as amostras.

É importante deixar claro que para utilizarmos esses métodos podemos usar tanto dados numéricos quanto categóricos. Além disso, não é necessário padronizar os dados.

Árvores de Decisão

Uma árvore de decisão, em geral, pergunta uma questão e classifica o elemento baseado na resposta. Ela utiliza os dados de cada indivíduo para criar uma regra de separação, que posteriormente será utilizada para rotular novas amostras.

As árvores de decisão podem ser aplicadas aos problemas de regressão e classificação. Primeiro vamos considerar os problemas de classificação, e depois passamos para a regressão.

em Classificação

Vejamos a seguir um exemplo de árvore de decisão para um problema de classificação.

Nomenclatura:

• Nó Raiz ou Raiz: é a variável que se encontra no topo da árvore;
• Nós Internos ou Nós: são as variáveis intermediárias, que possuem tanto setas apontandas para elas como saindo delas;
• Nós Folhas ou Nós Terminais ou Folhas: possuem apenas setas apontadas para elas. Representam a decisão final da árvore.

No processo de construção de uma árvore de decisão é importante ressaltar que a separação dos dados deve envolver apenas duas respostas: “Sim” ou “Não”. Também é preciso definir a ordem das variáveis, como a variável com que se deve começar, qual deve ser a seguinte, e assim por diante. A solução para isso é obtida através do nível de impureza das variáveis.

Dizemos que uma variável é impura quando ela não consegue separar bem os dados em uma árvore de decisão. Para calcularmos a impureza de uma variável utilizamos o indíce Gini, que varia entre 0 (mais puro possível) e 0,5 (mais impuro possível). Primeiramente calculamos o índice Gini para cada nó da variável, e em seguida obtemos o índice Gini da variável como uma média ponderada. O índice Gini de um nó é obtido por: \[\hbox{Gini(nó)} = 1 – {p_S}^{2} – {p_N}^{2}.\] onde \(p_S\) é a proporção de “sim” da resposta da variável de interesse e \(p_N\) a proporção de “não” da resposta da variável de interesse.

O índice Gini da variável é dado pela média do índice Gini para os nós referentes às respostas “Sim” e “Não” ponderada pela proporção dos elementos em cada nó.

\[ \hbox{Gini(variável)} = \hbox{Gini(nó}_1) \times P_1 + \hbox{Gini(nó}_2) \times P_2 \]

onde \(P_1\) é a proporção de elementos no 1º nó e \(P_2\) é a proporção de elementos no 2º nó.

Vamos construir uma árvore de decisão utilizando a base SmallHeart.

base = readRDS("SmallHeart.rds")
head(base)

Nosso objetivo é prever se um indivíduo tem ou não uma doença cardíaca (variável “HeartDisease”), baseado nas outras variáveis. As variáveis explicativas são as seguintes:

• Sex: indica o sexo do indivíduo, onde “M” = Masculino e “F” = Feminino;
• ChestPain: referente ao indivíduo sentir dor no peito, onde “typical” = típico e “nontypical” = não típico;
• Thal: indica se o indivíduo possui Talassemia, onde “normal” = não possui, “fixed” = talassemia irreversível e “reversable” = talassemia reversível.

Vamos verificar o quão bem as variáveis isoladamente são capazes de prever se o paciente possui ou não doença cardíaca. Vamos começar pela variável “Sex”.

summary(base$Sex)

Note que temos 22 indivíduos do sexo feminino e 50 indivíduos do sexo masculino. Como a resposta de um nó da árvore deve ser “Sim” ou “Não”, vamos utilizar a variável “Sex=M”.

# Verificando quantos indivíduos possuem doença cardíaca de acordo com o sexo:

base %>% group_by(Sex, HeartDisease) %>% summarise(N=n())

Então a variável “Sex=M” separa os pacientes da seguinte forma:

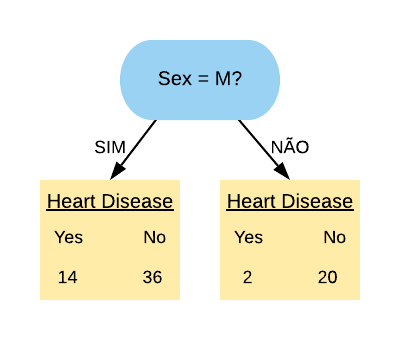
Note que a maioria dos pacientes com doença cardíaca terminaram na folha referente ao sexo masculino, mas a maioria dos que não possuem doença também. Já podemos ter uma ideia que essa variável não é tão boa em separar os dados, mas para averiguarmos essa hipótese vamos calcular o índice gini dela.

Primeiramente vamos calcular o índice Gini do nó “Sex = M Sim”:

\[ \hbox{Gini(Sex = M Sim)} = 1- \left( \frac{14}{50} \right)^{2} – \left( \frac{36}{50} \right)^{2} = 0,403.\]

Agora vamos calcular o índice Gini do nó “Sex = M Não”:

\[ \hbox{Gini(Sex = M Não)} = 1- \left( \frac{2}{22} \right)^{2} – \left( \frac{20}{22} \right)^{2} = 0,166.\]

O índice Gini da variável “Sex = M” é dado pela média do índice Gini dos nós referentes às respostas “Sim” e “Não” ponderada pela frequência dos indivíduos em cada nó.

\[ \hbox{Gini(Sex = M)} = 0,403 \times \frac{50}{72} + 0,166 \times \frac{22}{72} = 0,331.\]

Como o índice Gini da variável “Sex = M” ficou mais próximo de 0,5 do que de 0, podemos constatar que ela é uma variável com baixa pureza. Note que se tivéssemos escolhido a variável “Sex = F” o índice Gini obtido seria o mesmo, pois “Sex = F Sim” é equivalente a “Sex = M Não” e “Sex = F Não” é equivalente a “Sex = M Sim”. ou seja, as contas seriam as mesmas.

Agora vamos realizar o mesmo processo para a variável “ChestPain”, ou seja, vamos verificar o quão bem ela é capaz de prever se o paciente possui doença cardíaca.

base %>% group_by(ChestPain) %>% summarise(N=n())

Note que temos 23 indivíduos que sentem dor no peito tipicamente e 49 indivíduos que não sentem tipicamente. Vamos verificar quantos deles possuem doença cardíaca:

base %>% group_by(ChestPain, HeartDisease) %>% summarise(N=n())

Vamos considerar a variável “ChestPain = Typical”. Ela separa os dados da seguinte forma:

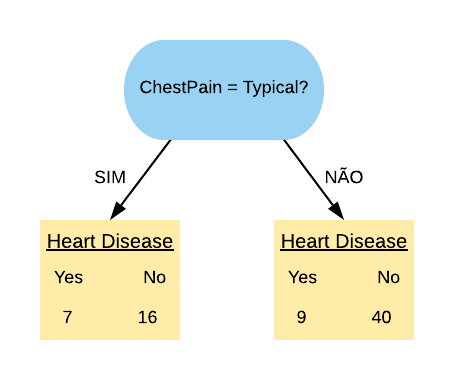
Note que quase metade dos pacientes que possuem dor no peito têm doença cardíaca. Dos que não sentem a dor no peito, quase \(\frac{1}{4}\) apenas possui a doença.

Vamos calcular o índice Gini do nó “ChestPain = Typical Sim”:

\[ \hbox{Gini(ChestPain = Typical Sim)} = 1- \left( \frac{7}{23} \right)^{2} – \left( \frac{16}{23} \right)^{2} = 0,423.\]

Agora vamos calcular o índice Gini do nó “ChestPain = Typical Não”:

\[ \hbox{Gini(ChestPain = Typical Não)} = 1- \left( \frac{9}{49} \right)^{2} – \left( \frac{40}{49} \right)^{2} = 0,299.\]

O índice Gini da variável “ChestPain = Typical” é dado pela média do índice Gini dos nós referentes às respostas “Sim” e “Não” ponderada pela frequência dos indivíduos em cada nó.

\[ \hbox{Gini(ChestPain = Typical)} = 0,423 \times \frac{23}{72} + 0,299 \times \frac{49}{72} = 0,339.\]

Note que ela obteve um índice Gini um pouco maior do que a variável “Sex = M”. Isso indica que a variável “Sex = M” é mais pura do que a variável “ChestPain = Typical”.

Agora falta apenas obter o índice Gini da variável “Thal”. Mas diferentemente das outras 2 ela não possui apenas 2 níveis, e sim 3: “normal”, “fixed” e “reversable”.

library(dplyr)
base %>% group_by(Thal) %>% summarise(N=n())

Nesse caso vamos ter que calcular o índice Gini para todas as combinações possíveis: “Thal = normal”, “Thal = fixed”, “Thal = reversable”, “Thal = normal ou fixed”, “Thal = normal ou reversable”, “Thal = fixed ou reversable”. Porém note que o índice Gini da variável “Thal = normal” é equivalente ao da variável “Thal = fixed ou reversable”, pois “Thal = normal Sim” é o mesmo que “Thal = fixed ou reversable Não”. Da mesma forma isso vale para as variáveis “Thal = fixed” e “Thal = normal ou reversable”, e “Thal = reversable” e “Thal = normal ou fixed”. Com isso conseguimos economizar algumas contas.

base %>% group_by(Thal, HeartDisease) %>% summarise(N=n())

Vamos, primeiramente, olhar para a variável “Thal = normal”. Ela separa os dados da seguinte forma:

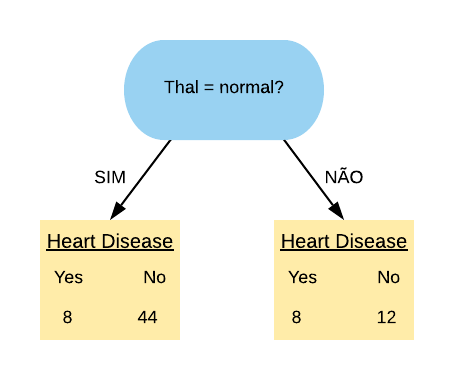
Note que a maioria dos pacientes que possuem doença cardíaca estão no grupo dos que possuem “Thal = normal”.

Vamos calcular o índice Gini do nó “Thal = Normal Sim”:

\[ \hbox{Gini(Thal = Normal Sim)} = 1- \left( \frac{8}{52} \right)^{2} – \left( \frac{44}{52} \right)^{2} = 0,26.\]

Agora vamos calcular o índice Gini do nó “Thal = Normal Não”:

\[ \hbox{Gini(Thal = Normal Não)} = 1- \left( \frac{8}{20} \right)^{2} – \left( \frac{12}{20} \right)^{2} = 0,48.\]

Então o índice Gini da variável “Thal = Normal” fica da seguinte forma:

\[ \hbox{Gini(Thal = Normal)} = 0,26 \times \frac{52}{72} + 0,48 \times \frac{20}{72} = 0,321.\]

Agora vamos olhar para a variável “Thal = Fixed”. Ela separa os dados da seguinte forma:

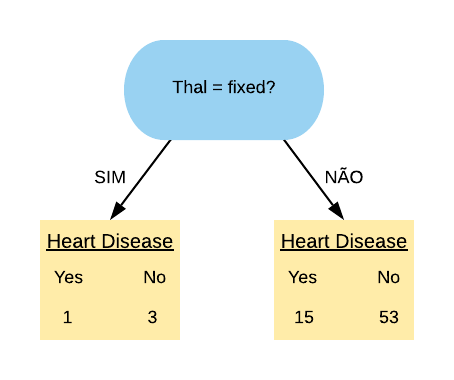
Vamos calcular o índice Gini do nó “Thal = Fixed Sim”:

\[ \hbox{Gini(Thal = Fixed Sim)} = 1- \left( \frac{1}{4} \right)^{2} – \left( \frac{3}{4} \right)^{2} = 0,375.\]

Agora vamos calcular o índice Gini do nó “Thal = Fixed Não”:

\[ \hbox{Gini(Thal = Fixed Não)} = 1- \left( \frac{15}{68} \right)^{2} – \left( \frac{53}{68} \right)^{2} = 0,344.\]

Então o índice Gini da variável “Thal = Fixed” fica da seguinte forma:

\[ \hbox{Gini(Thal = Fixed)} = 0,375 \times \frac{4}{72} + 0,344 \times \frac{68}{72} = 0,346.\]

Por último, vamos olhar para a variável “Thal = Reversable”.

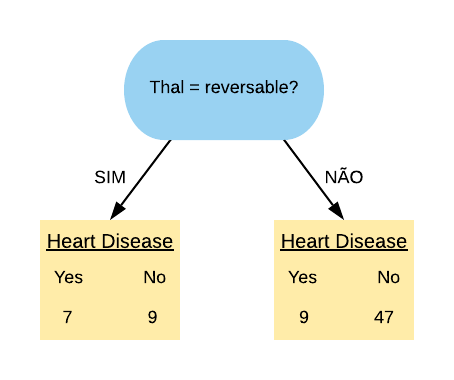
Vamos calcular o índice Gini do nó “Thal = Reversable Sim”:

\[ \hbox{Gini(Thal = Reversable Sim)} = 1- \left( \frac{7}{16} \right)^{2} – \left( \frac{9}{16} \right)^{2} = 0,492.\]

Agora vamos calcular o índice Gini do nó “Thal = Reversable Não”:

\[ \hbox{Gini(Thal = Reversable Não)} = 1- \left( \frac{9}{56} \right)^{2} – \left( \frac{47}{56} \right)^{2} = 0,269.\]

Então o índice Gini da variável “Thal = Reversable” fica da seguinte forma:

\[ \hbox{Gini(Thal = Reversable)} = 0,492 \times \frac{16}{72} + 0,269 \times \frac{56}{72} = 0,319\]

Resumindo, os índices Ginis de todas as variáveis são:

gini = tibble("Variáveis" = c("Sex = M", "ChestPain = Typical", "Thal = Normal", "Thal = Fixed", "Thal = Reversable"), "Índice Gini" = c("0,331", "0,339", "0,321", "0,346", "0,319"))

knitr::kable(gini)

A variável “Thal = Reversable” é a que possui o menor índice Gini, portanto ela é a mais pura. Ela ficará no topo da árvore de decisão, ou seja, será o nó raiz.

O próximo passo é definir as variáveis que ficarão no nó “Thal = Reversable Sim” e “Thal = Reversable Não”. Para isso temos que olhar para a base de dados com os indivíduos do grupo “Thal = Reversable Sim” e “Thal = Reversable Não”, respectivamente.

# Grupo de indivíduos "Thal = Reversable Sim":
base1 = base %>% filter(Thal == "reversable")
head(base1)

Agora temos que calcular o índice Gini para todas as variáveis referentes a esse grupo. A que for mais pura entrará no nó “Thal = Reversable Sim”. Poupando os cálculos, vamos obter que o menor índice Gini é o da variável “ChestPain = Typical”.

# Grupo de indivíduos "Thal = Reversable Não":
base2 = base %>% filter(Thal != "reversable")
head(base2)

Agora calculamos também o índice Gini para todas as variáveis referentes a esse grupo. Após os cálculos necessários veremos que o menor índice Gini é o da variável “ChestPain = Nontypical”.

Dessa forma, podemos dar continuidade a nossa árvore.

Após obtidos esses novos nós, o processo continua se repetindo, obtendo novos nós e/ou folhas para a árvore, até a construção chegar ao fim.

Pergunta: quando o processo de construção de uma árvore chega ao fim? O processo de construção pode terminar por 3 fatores:

1. Quando a pureza do nó é maior do que o de qualquer variável que adicionamos;
2. Quando atingimos folhas 100% puras (índice Gini = 0);
3. Quando o ganho ao aumentar a árvore é muito pequeno.

O ganho ao aumentar a árvore pode ser resumido como um conjunto de atributos presentes na árvore que retornem o maior ganho de informações. Essa questão será melhor abordada posteriormente, juntamente com a questão de como podar as árvores (que está intimamente relacionada ao ganho) no subcapítulo XGBoost.

em Regressão

Agora iremos discutir o processo de construção de uma árvore de regressão. Em uma árvore de regressão, diferentemente de uma árvore para classificação, cada folha possui um valor numérico (ao invés de categorias como “Sim” ou “Não”, como no exemplo anterior da base SmallHeart). Vejamos a seguir um exemplo de árvore de decisão para um problema de regressão.

Esse valor numérico presente nas folhas não é nada menos que a média do valor da variável de interesse a ser prevista para os elementos que satisfazem a condição do nó. Por exemplo, na árvore de regressão acima a primeira folha dá como resultado uma eficácia de 5%: essa foi a média observada da eficácia do medicamento em pacientes com mais de 50 anos de idade. Para a segunda folha, a com eficácia de 20%: esse valor é a média da eficácia do medicamento em um indivíduo com menos de 50 anos de idade e que toma uma dosagem maior do que 29mg foi de 20%. O processo é o mesmo para as outras folhas.

A grande pergunta é qual valor colocar no nó como condição. Para exemplificar como funciona o processo, vamos começar com um exemplo simples:

Ex.: Vamos carregar o banco de dados “SmallAdvertising”. Este banco possui informações sobre as vendas de um produto em 10 mercados diferentes (variável sales), além de orçamentos de publicidade para esse produto em cada um dos mercados para três mídias diferentes: TV, rádio e jornal (variáveis TV, radio e newspaper, respectivamente).

vendas = readRDS("SmallAdvertising.rds")
vendas

Vamos considerar o caso em que queremos construir uma árvore de regressão para prever as vendas baseados apenas na variável TV.

plot(vendas$TV, vendas$sales, pch = 19,
     xlab = "Orçamento de Publicidade do Produto para a TV",
     ylab = "Vendas do Produto",
     main = "Vendas do produto x Publicidade para a TV")

Primeiramente é preciso definir qual valor irá entrar como condição no primeiro nó. O algoritmo realiza isso testando todos os possíveis valores de separação para os dados, e pega o que minimiza a soma dos quadrados dos resíduos. Inicialmente, como o primeiro separador, ele considera a média dos 2 menores valores da Publicidade.

ordenados = sort(vendas$TV)
mean(ordenados[1:2])

Então 44,95 é o primeiro valor a ser testado para a separação dos dados.

plot(vendas$TV, vendas$sales, pch = 19,
     xlab = "Orçamento de Publicidade do Produto para a TV",
     ylab = "Vendas do Produto",
     main = "Vendas do produto x Publicidade para a TV"); abline(v = 44.95,
                                                                 col = "red")

Assim, o primeiro nó será da seguinte forma:

<img src="http://cienciadedados.uff.br/wp-content/uploads/sites/195/2020/04/image-6.png" alt="Figura 11: Divisão por 'TV

Para a resposta “sim” prevemos que as vendas do produto será de 9,2, o qual é o resultado da média dos valores das vendas para todos os produtos cuja publicidade foi menor do que 44,95 (ou seja, é apenas o valor do primeiro elemento). Para a resposta “Não”, então a folha seguinte contém o resultado da média dos valores das vendas para todos os produtos cuja publicidade foi maior do que 44,95, o qual é de 15,05.

Note que fazendo isso teremos resíduos (diferença do valor original e do valor predito pela árvore) muito grandes. O algoritmo eleva esses resíduos ao quadrado e os soma. Esse valor é a soma dos quadrados dos resíduos considerando o nó “Publicidade para a TV < 44,95?”.

Em seguida ele irá para o próximo separador: a média do segundo e do terceiro menores pontos.

mean(ordenados[2:3])

Então 66,95 é o segundo valor a ser testado para a separação dos dados.

plot(vendas$TV, vendas$sales, pch = 19,
     xlab = "Orçamento de Publicidade do Produto para a TV",
     ylab = "Vendas do Produto",
     main = "Vendas do produto x Publicidade para a TV"); abline(v = 66.95,
                                                                 col = "red")

Então o nó considerado será da forma “Publicidade para a TV < 66,95?”.

<img src="http://cienciadedados.uff.br/wp-content/uploads/sites/195/2020/04/image-8.png" alt="Figura 12: Divisão por 'TV

O valor de 8,9 corresponde ao resultado da média dos valores das vendas para todos os produtos cuja publicidade foi menor do que 66,95. Então a árvore prevê esse valor de vendas para o produto que obteve uma publicidade para a TV < 66,95. O valor de 15,77 é o resultado da média dos valores das vendas para todos os produtos cuja publicidade foi maior do que 66,95. Novamente serão obtidos os resíduos dessa predição e eles serão somados.

Então o algoritmo irá para o próximo separador e irá calcular a soma dos quadrados dos resíduos da predição. Isso ocorre sucessivamente até acabarem todos os separadores possíveis para a árvore. O separador vencedor (aquele que irá para o nó raiz) é aquele com a menor soma dos quadrados dos resíduos.

A construção dos próximos nós se dá pela mesma forma que a do nó raiz. O processo de construção da árvore termina quando:

1. Atingimos um número mínimo de observações em uma folha (usualmente é utilizado 20 observações). Não continuamos a divisão após esse número mínimo pois corremos o risco de criar uma árvore sobreajustada à amostra dada;
2. Quando o ganho ao aumentar a árvore é muito pequeno.

Agora vamos para o caso em que tenhamos mais de uma variável preditiva nos dados. Vamos considerar agora que queremos prever as vendas do produto baseado em seus orçamentos de publicidade para TV, rádio e jornal.

Assim como anteriormente, começamos usando o orçamento para a TV para prever as vendas, e pegamos o separador com a menor soma dos quadrados dos resíduos. O melhor separador se torna um candidato para a raiz da árvore. Em seguida, focamos em utilizar o orçamento para o rádio para prever as vendas. Assim como com o orçamento para a TV, tentamos diferentes separadores para a predição e calculamos a soma dos quadrados dos resíduos em cada passo. O melhor separador se torna outro candidato para a raiz. Por último, utilizamos o orçamento para o jornal para prever as vendas, e após tentarmos diferentes separadores pegamos aquele com a menor soma dos quadrados dos resíduos também. Então comparamos a soma dos quadrados dos resíduos de todos os candidatos para a raiz, e o escolhido, novamente, é aquele com a menor soma.

Para os próximos nós o processo de construção também é equivalente ao anterior, exceto que agora nós comparamos a menor soma dos quadrados dos resíduos de cada preditor. E, novamente, quando uma folha atinge um número mínimo de observações, a árvore é finalizada.

Construindo árvores com o rpart e rpart.plot

Vamos construir árvores com o comando rpart(). Como argumento da função nós passamos:

1. A variável de interesse a ser prevista em função das variáveis preditoras;
2. A base de dados onde as variáveis se encontram.

Vamos utilizar a base de dados referentes ao primeiro exemplo dado de construção de uma árvore, onde queríamos prever se um indivíduo possui doença cardíaca baseado em características dele.

library(rpart)
heart_arvore = rpart(HeartDisease~., data = base)

Agora vamos plotar a árvore com o comando rpart.plot().

library(rpart.plot)
rpart.plot(heart_arvore)

Observe que a árvore ficou “vazia”. O que ela quer dizer com isso é: assuma “Não” sempre para o indivíduo possuir doença cardíaca, e acerte com precisão de 78%. Isso ocorre devido aos valores iniciais do comando rpart.control(), que ajusta os parâmetros da função rpart(). Os principais parâmetros do rpart.control são:

• minsplit: o número mínimo de observações que devem existir em um nó para que uma divisão seja tentada. Padrão: minsplit = 20;
• minbucket: o número mínimo de observações em qualquer folha. Padrão: minbucket = minsplit/3;
• cp (complexity parameter): o mínimo de ganho de ajuste que devemos ter em cada divisão. O principal papel desse parâmetro é economizar tempo de computação removendo as divisões que não valem a pena. Padrão: cp = 0,01;
• maxdepth: profundidade máxima da árvore (a profundidade da raiz é zero). Não pode ser maior que 30.

Ex. 1: Vamos ajustar os parâmetros da árvore e construí-la novamente. Vamos determinar que a profundidade da árvore seja 2, que 0 seja o número mínimo de observações em um nó e que ela seja construída mesmo que não haja ganhos em mais divisões.

controle = rpart.control(minsplit=0, cp = -1, maxdepth = 2)
heart_arvore = rpart(HeartDisease~., data = base, control = controle)
rpart.plot(heart_arvore)

Note que o nó raiz é exatamente aquele que calculamos como o mais puro, o “Thal = Reversable”, que é equivalente a “Thal = Fixed ou Normal”. Os nós adjacentes também foram o que obtivemos anteriormente como os mais puros.

Cada saída do comando rpart.plot() tem um significado específico:

1. A primeira saída é a classe estimada pela árvore para as amostras que se encontram naquele nó.

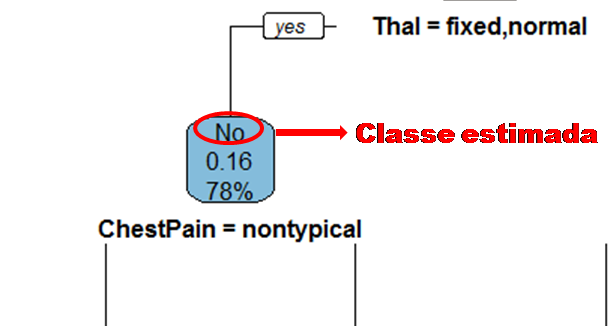
1. A segunda saída é a proporção de indivíduos na classe contrária àquela estimada na primeira saída.

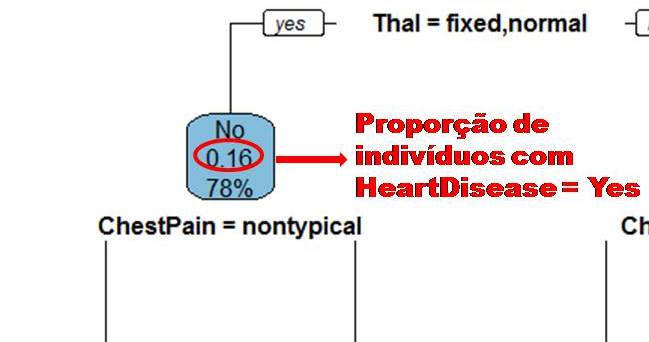
1. A terceira saída é a porcentagem da amostra que se encontra no atual nó.

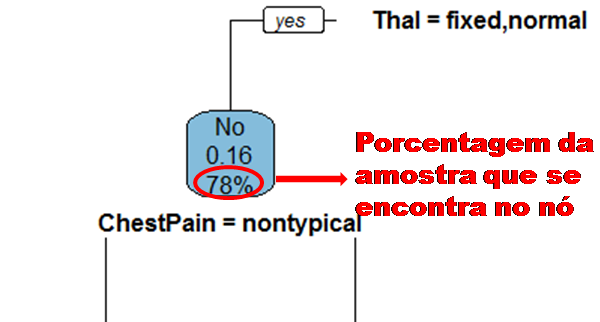
Ex. 2: Vamos agora constuir a árvore mais completa possível, ou seja, uma árvore sobreajustada à amostra, sem restrições em sua profundidade máxima.

controle = rpart.control(minsplit=0, cp = -1)
heart_arvore = rpart(HeartDisease~., data = base, control = controle)
rpart.plot(heart_arvore)

Ex. 3: Vamos agora considerar 10 como o número mínimo de observações em um nó e 3 como a profundidade máxima da árvore.

controle = rpart.control(minsplit=10, cp = -1, maxdepth = 4)
heart_arvore = rpart(HeartDisease~., data = base, control = controle)
rpart.plot(heart_arvore)

Agora podemos levantar a seguinte questão: como avaliar a precisão do modelo construído? Nesse exemplo nós utilizamos toda a amostra para construir a árvore, apenas para explicar o funcionamente do rpart, então não temos uma amostra teste para verificar o quão bom é o modelo. Então para isso teríamos que primeiramente dividir a amostra em treino e teste, depois criar o modelo com a amostra treino e em seguida aplicá-lo na amostra teste, e então, por último, poderíamos utilizar a função confusionMatrix() para obtermos não só a precisão como outras medidas avaliativas do modelo, além, é claro, da matriz de confusão. No tópico abaixo essas etapas serão construídas detalhadamente.

Árvores com train {#link8}

Podemos utilizar árvores de decisão/regressão como um método de treinamento para os dados através da função train(). Vamos fazer isso utilizando a base de dados College. Este banco possui informações sobre 777 diferentes universidades e faculdades dos EUA. Ela apresenta algumas variáveis como: Apps – número de pedidos recebidos para ingresso, Room.Board – custos de acomodação e alimentação, Books – custos estimados de livros, PhD – quantidade de professores com doutorado, entre outras, e nossa variável de interesse Private, que indica se a universidade é privada ou pública.

library(readr)
college = read_csv2("College.csv")
head(college)

Vamos, primeiramente, separar a amostra em treino e teste.

library(caret)
set.seed(100)
noTreino = createDataPartition(y = college$Private, p = 0.7, list = F)
treino = college[noTreino,]
teste = college[-noTreino,]

Vamos treinar o modelo pelo método de árvores de decisão. Fazemos isso através do argumento “method = rpart” da função train().

set.seed(100)
modelo = caret::train(Private~., method = "rpart", data = treino)
modelo

Observe que através do train() são testados alguns valores para o cp (complexity parameter) e é eleito aquele com a maior taxa de acurácia. Nesse caso, o cp utilizado será o de aproximadamente 0,0436. Vamos aplicar o modelo no conjunto teste.

predicao = predict(modelo, teste)

# Transformando em fator para depois construirmos a matriz de confusão:
teste$Private = as.factor(teste$Private)

# Avaliando o modelo utilizando a matriz de confusão:
confusionMatrix(predicao, teste$Private)

Obtivemos uma acurácia de 0,8922, o que é razoável para um modelo que utiliza árvores.

# Desenhando a árvore:
rpart.plot(modelo$finalModel)

A limitação de utilizar as árvores através do train() é que o único parâmetro da árvore que pode ser alterado é o cp (complexity parameter).

modelLookup("rpart")

Para alterarmos o seu valor utilizamos o comando expand.grid().

controle = expand.grid(.cp = 0.0001)
modelo = caret::train(Private~., method = "rpart", data = treino, tuneGrid = controle)
modelo

Note que com esse valor de cp a árvore fica mais profunda, pois estamos diminuindo o mínimo de ganho de ajuste que devemos ter em cada divisão.

rpart.plot(modelo$finalModel)

---

Florestas Aleatórias

As árvores de decisão possuem uma estrutura de fácil compreensão, o que faz com que ela seja bastante utilizada devido a sua boa aparência e interpretação intuitíva. Mas elas possuem uma limitação, o sobreajuste, sendo assim, elas não são muito eficientes com novas amostras. O que fazer então?

As Florestas Aleatórias (Random Forest) se utilizam de várias árvores de decisão, combinando a simplicidade das árvores com a flexibilidade de um método sem sobreajuste, aumentando assim a precisão do preditor.

Vamos construir uma floresta aleatória usando a base de dados balloons.

balloons = readr::read_csv("balloons.csv")
balloons$Inflated = as.factor(balloons$Inflated)
str(balloons)

Com base na cor do balão, o tamanho dele, se ele é elástico ou não e se quem o está enchendo é uma criança ou um adulto, queremos predizer se o balão vai encher ou não. Portanto, nossa variável de interesse é Inflated e queremos construir um classificador.

A primeira coisa que precisamos fazer é criar uma nova amostra do mesmo tamanho da original utilizando bootstrap.

set.seed(33)
boot1 = caret::createResample(y=balloons$Inflated, times=1, list=F)
NovaAmostra1 = balloons[boot1,]
Out_of_bag = balloons[-boot1,]

Todas as observações que não forem sorteadas vão entrar no “Out-of-Bag”. Temos 4 variáveis fora a de interesse, vamos sortear 2 variáveis para construir o primeiro nó da nossa árvore.

set.seed(413)
sample(1:4, 2)

Vamos calcular o índice Gini para essas duas variáveis.

#calculando o indice gini para a variável tamanho
table(NovaAmostra1$Size, NovaAmostra1$Inflated)
(gini.size = (1-(7/14)^2-(7/14)^2)*(14/20) + (1-(4/6)^2-(2/6)^2)*(6/20))
#calculando o indice gini para a variável idade
table(NovaAmostra1$Age, NovaAmostra1$Inflated)
(gini.age = (1-(5/14)^2-(9/14)^2)*(14/20) + (1-(6/6)^2-(0/6)^2)*(6/20))

A variável idade tem um grau de impureza menor, então ela será a raiz da árvore.

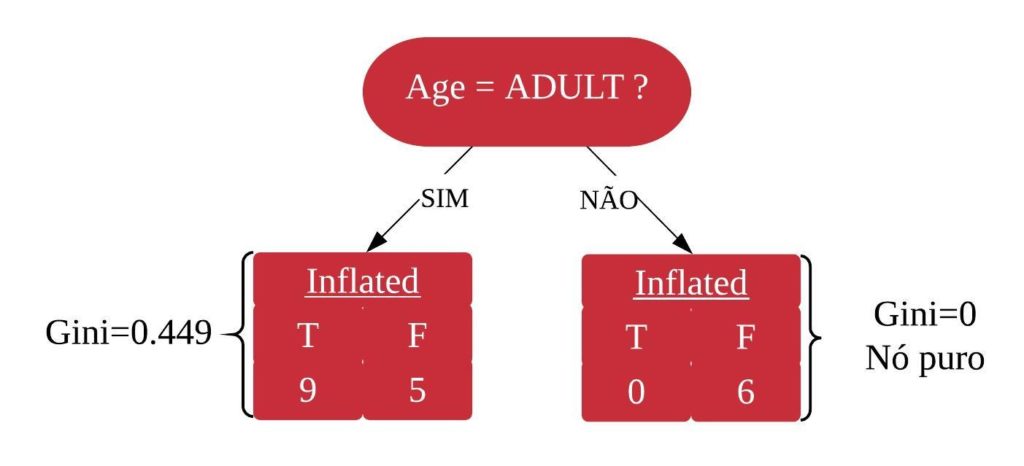
{width=60%}

Agora das variáveis que ainda não foram usadas, sorteamos mais duas para continuar a árvore.

set.seed(443)
sample(1:3, 2)

library(dplyr)
NovaAmostra1 = filter(NovaAmostra1, Age=="ADULT") 
#calculando o indice gini para a variável tamanho
table(NovaAmostra1$Size, NovaAmostra1$Inflated)
(gini.size = (1-(4/11)^2-(7/11)^2)*(11/14) + (1-(1/3)^2-(2/3)^2)*(3/14))
#calculando o indice gini para a variável act
table(NovaAmostra1$Act, NovaAmostra1$Inflated)
(gini.act = (1-(5/5)^2-(0/5)^2)*(5/14) + (1-(0/9)^2-(9/9)^2)*(9/14))

Como a variável act tem o menor grau de impureza, ela será o próximo nó.

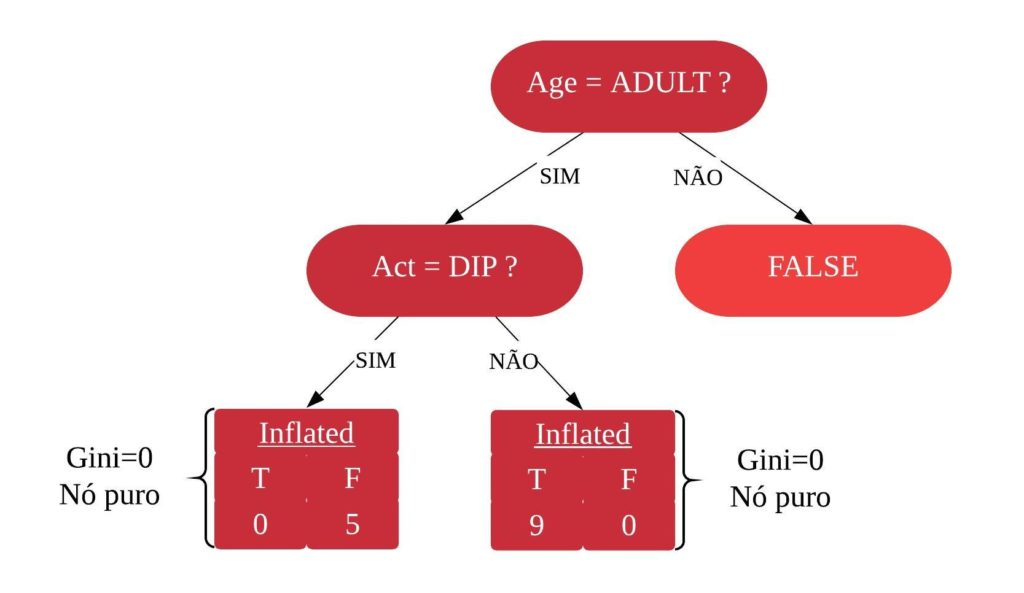
{width=60%}

Assim, temos nossa primeira árvore de decisão.

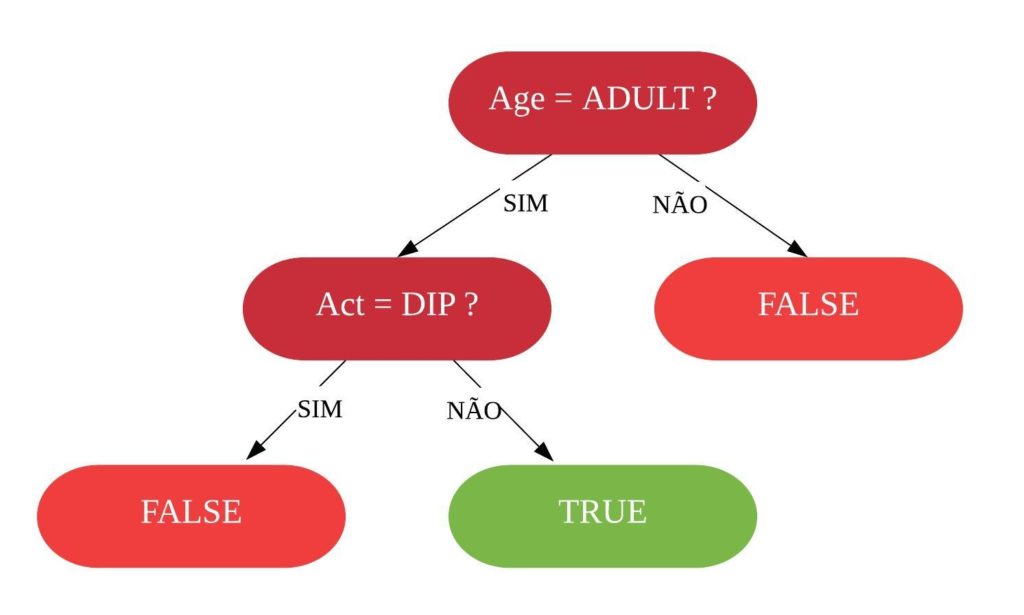
{width=60%}

Em seguida vamos construir várias árvores da mesma maneira que a anterior. Para nosso exemplo vamos construir apenas 4 árvores, mas em geral vamos fazer bem mais que isso.

Temos então nossas 4 árvores construidas.

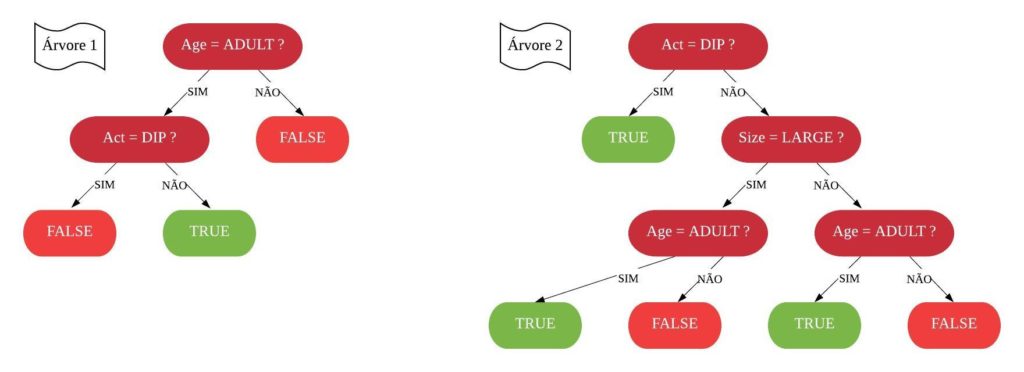
{width=90%}

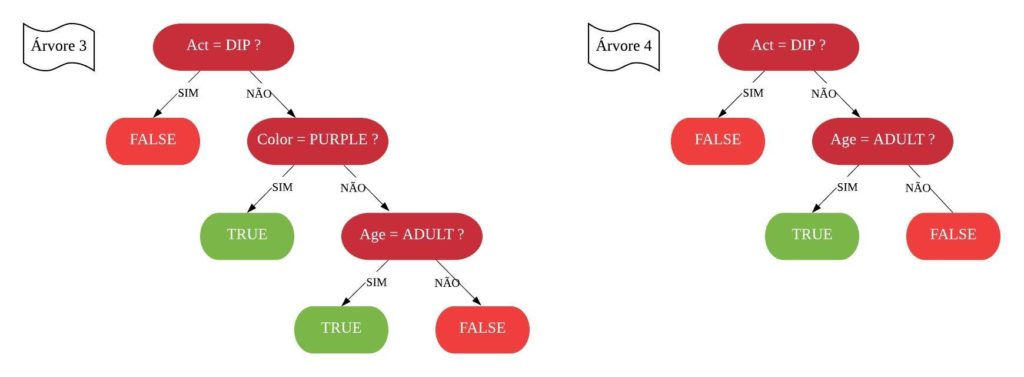
{width=90%}

Para classificar uma nova amostra, devemos passar ela por todas as árvores construidas e rotular a amostra pela categoria resultada mais vezes.

O método de usar bootstrap para criar novas amostras e votos para a tomada de decisão é chamado de Bagging (**Bootstrap+aggregate).

As observações de cada amostra que não entraram na construção de cada árvore estão contidas Out_of_bag. Essas observações servirão para avaliar nosso preditor.

Out_of_bag = balloons[c(2,4,12,13,15,18,20,
                        1,2,3,5,10,
                        2,4,12,13,15,18,20,
                        2,3,11,13,14,16,19),]
knitr::kable(Out_of_bag)

Para avaliar, é preciso passar cada uma das observações do Out_of_bag por todas as árvores e a predição será feita por votos também. Ao fazer isso, observamos uma precisão de 86%.

A proporção de amostras do Out-of-bag que foram incorretamente classificadas é chamada Out-of-bag-error

Agora que sabemos avaliar o modelo, podemos comparar florestas aleatórias construídas com 2 variáveis com as construídas com 3 e outras diferentes configurações. Tipicamente, começamos usando o quadrado do número de variáveis da base e tentamos algumas quantidades abaixo e acima.

Construindo uma floresta com o randomForest()

O pacote randomForest possui as ferramentas adequadas para a criação de uma floresta aleatória. Vamos construir uma floresta com 20 árvores utilizando a base balloons.

É importante observar se as váriaveis categóricas estão na classe de fatores.

balloons = readr::read_csv("balloons.csv")
# tratando todas as variaveis 
balloons = dplyr::mutate_if(balloons, is.character, as.factor)
balloons$Inflated = as.factor(balloons$Inflated)
# construindo floresta com 20 arvores
library(randomForest)
set.seed(23)
modelo = randomForest(Inflated ~ ., data=balloons, ntree=20)

Agora, vamos avaliar a precisão do modelo.

# avaliando o modelo
modelo

Note que foram construídas 20 árvores utilizando 2 variáveis a cada vez. Essa quantidade de variáveis pode ser alterada usando o argumento mtry= dentro do randomForest.

Podemos ver que a precisão do nosso modelo é de 19/20, ou seja, 95%. Qual seria a precisão se fosse feito apenas uma árvore?

balloons = readr::read_csv("balloons.csv")
# tratando todas as variaveis 
balloons = dplyr::mutate_if(balloons, is.character, as.factor)
balloons$Inflated = as.factor(balloons$Inflated)
# separando amostras teste/treino
set.seed(45)
inTrain = caret::createDataPartition(balloons$Inflated,p=0.5,list=F)
treino = balloons[inTrain,]
teste = balloons[-inTrain,]
# treinando o modelo
modFit = caret::train(Inflated~., method="rpart", data=balloons)
# aplicando o modelo no teste
predicao = predict(modFit,teste)
# avaliando o erro na amostra treino
confusionMatrix(teste$Inflated,predicao)

Note que nessa árvore, nosso modelo teve uma precisão de 80%. Bem menor do que o modelo de florestas.

Agora, observe que construimos uma floresta com 20 árvores. O que acontece com o erro do modelo conforme acrescentamos mais árvores?

Vamos avaliar o comportamento do erro conforme acrescentamos mais árvores à floresta. Para isso, utilizaremos a base de dados spam para melhor vizualização

# chamando a base
library(kernlab)
data("spam")
# construindo floresta com 20 arvores
library(randomForest)
set.seed(23)
modelo = randomForest(type ~ ., data=spam, ntree=20)

# observando o comportamento do erro em 20 árvores
erro_OOB <- data.frame(
  Arvores = rep(1:nrow(modelo$err.rate), times=2),
  Type = rep(c("spam", "nonspam"), each=nrow(modelo$err.rate)),
  Erro = c(modelo$err.rate[,"spam"], modelo$err.rate[,"nonspam"]))

ggplot(data=erro_OOB, aes(x=Arvores, y=Erro)) +
  geom_line(aes(color=Type),size=1.1)

# construindo floresta com 50 arvores
set.seed(23)
modelo = randomForest(type ~ ., data=spam, ntree=50)
# observando o comportamento do erro em 50 árvores
erro_OOB <- data.frame(
  Arvores=rep(1:nrow(modelo$err.rate), times=2),
  Type=rep(c("spam", "nonspam"), each=nrow(modelo$err.rate)),
  Erro=c(modelo$err.rate[,"spam"],
          modelo$err.rate[,"nonspam"]))

ggplot(data=erro_OOB, aes(x=Arvores, y=Erro)) +
  geom_line(aes(color=Type),size=1.1)

# construindo floresta com 100 arvores
set.seed(23)
modelo = randomForest(type ~ ., data=spam, ntree=100)
# observando o comportamento do erro em 100 árvores
erro_OOB <- data.frame(
  Arvores=rep(1:nrow(modelo$err.rate), times=2),
  Type=rep(c("spam", "nonspam"), each=nrow(modelo$err.rate)),
  Erro=c(modelo$err.rate[,"spam"],
          modelo$err.rate[,"nonspam"]))

ggplot(data=erro_OOB, aes(x=Arvores, y=Erro)) +
  geom_line(aes(color=Type),size=1.1)

# construindo floresta com 1000 arvores
set.seed(23)
modelo = randomForest(type ~ ., data=spam, ntree=1000)
# observando o comportamento do erro em 1000 árvores
erro_OOB <- data.frame(
  Arvores=rep(1:nrow(modelo$err.rate), times=2),
  Type=rep(c("spam", "nonspam"), each=nrow(modelo$err.rate)),
  Erro=c(modelo$err.rate[,"spam"],
          modelo$err.rate[,"nonspam"]))

ggplot(data=erro_OOB, aes(x=Arvores, y=Erro)) +
  geom_line(aes(color=Type),size=1.1)

Repare que após uma certa quantidade de árvores, o erro se estabiliza. Sendo assim, não é necessário utilizar grandes quantidades de árvores em todos os casos. É preciso verificar até onde existe ganho.

Construindo uma floresta com o train()

Também é possivel fazer florestas aleatórias usando a função train do pacote caret. Para isso, é necessário alterar o método de reamostragem para out of bag. Vamos utilizar a base spam para melhor visualização.

# alterando o metodo de reamostragem
controle = trainControl(method="oob")
# chamando a base
library(kernlab)
data(spam)
# construindo o modelo com 50 arvores
set.seed(534)
modelo = caret::train(type ∼ ., data=spam, method="rf", ntree=50, trControl=controle)
modelo

Note o valor “mtry” no modelo. Ele indica a quantidade de váriaveis da base que foram utilizadas. Repare que ele calcula a precisão e kappa para diferentes quantidades de variáveis usadas e utiliza no final a quantidade que possuir maior precisão, no caso mtry=29. Caso queira fixar o número de variáveis usadas, basta usar o seguinte comando.

tng = expand.grid(.mtry=7)
modelo = caret::train(type ∼ ., data=spam, method="rf", ntree=50, trControl=controle, tuneGrid=tng)
modelo

---

AdaBoost

O método de treino AdaBoost se baseia na construção de uma floresta aleatória. Entretanto, na floresta construída por esse método as árvores possuem apenas um nó e duas folhas. Essas árvores são chamadas de tocos.

Em geral, tocos não são muito bons em fazer classificações precisas, ou seja, eles são classificadores fracos. No entanto, o método AdaBoost os combina de forma a criar um bom aprendiz. Ele faz isso utilizando diferenciais na classificação e na construção das árvores que a floresta aleatória comum não utiliza:

• Floresta Aleatória: cada árvore de decisão tem um peso igual na classificação final das amostras. Além disso, cada árvore é construída independentemente das outras.
• AdaBoost: alguns tocos têm mais peso na classificação final do que outros, e a ordem de construção dos tocos importam. Em outras palavras, os erros que o primeito toco comete influenciam em como o segundo toco é construído, os erros que o segundo toco comete influenciam em como o terceiro toco é construído, e assim sucessivamente.

Vamos ver os detalhes práticos de como funciona o AdaBoost utilizando o banco de dados golf. Este banco possui informações sobre condições climáticas e se o indivíduo jogou golf no dia. A ideia é tentar prever se o indivíduo vai jogar golf baseado nas outras variáveis.

golf = readRDS("Golf.rds")
golf

Primeiramente construímos um toco para cada uma das variáveis e calculamos seus respectivos índices Gini. Vamos começar com a variável Outlook.

library(dplyr)
golf %>% group_by(Outlook, Play) %>% summarise(N=n())

Então temos que “Outlook = Overcast” separa os dados da seguinte forma:

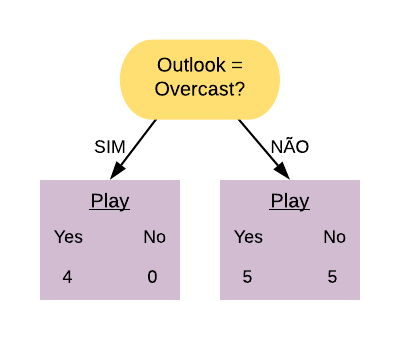
\(\hbox{Gini(Outlook = Overcast)} = \frac{4}{14} \times \left[ 1- \left( \frac{4}{4} \right)^{2} – \left( \frac{0}{4} \right)^{2} \right] + \frac{10}{14} \times \left[ 1- \left( \frac{5}{10} \right)^{2} – \left( \frac{5}{10} \right)^{2} \right] = 0,357.\)

Vamos agora olhar para “Outlook = Rain”:

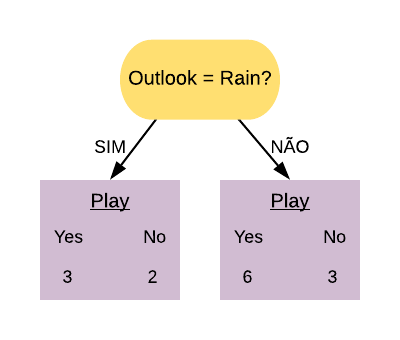
\(\hbox{Gini(Outlook = Rain)} = \frac{5}{14} \times \left[ 1- \left( \frac{3}{5} \right)^{2} – \left( \frac{2}{5} \right)^{2} \right] + \frac{9}{14} \times \left[ 1- \left( \frac{6}{9} \right)^{2} – \left( \frac{3}{9} \right)^{2} \right] = 0,457.\)

Por último, “Outlook = Sunny”:

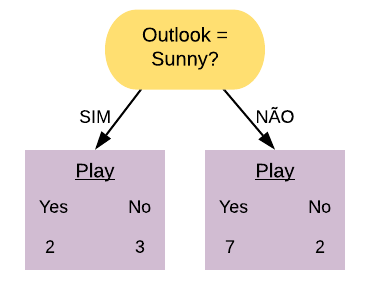
\(\hbox{Gini(Outlook = Sunny)} = \frac{5}{14} \times \left[ 1- \left( \frac{2}{5} \right)^{2} – \left( \frac{3}{5} \right)^{2} \right] + \frac{9}{14} \times \left[ 1- \left( \frac{7}{9} \right)^{2} – \left( \frac{2}{9} \right)^{2} \right] = 0,394.\)

Agora vamos para a variável Humidity.

golf %>% group_by(Humidity, Play) %>% summarise(N=n())

Temos que “Humidity = High” separa os dados da seguinte forma:

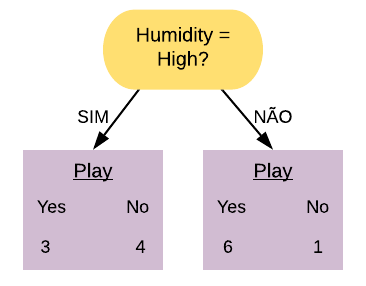
\(\hbox{Gini(Humidity = High)} = \frac{7}{14} \times \left[ 1- \left( \frac{3}{7} \right)^{2} – \left( \frac{4}{7} \right)^{2} \right] + \frac{7}{14} \times \left[ 1- \left( \frac{6}{7} \right)^{2} – \left( \frac{1}{7} \right)^{2} \right] = 0,367.\)

Por último, a variável Wind:

golf %>% group_by(Wind, Play) %>% summarise(N=n())

\(\hbox{Gini(Wind = Strong)} = \frac{6}{14} \times \left[ 1- \left( \frac{3}{6} \right)^{2} – \left( \frac{3}{6} \right)^{2} \right] + \frac{8}{14} \times \left[ 1- \left( \frac{6}{8} \right)^{2} – \left( \frac{2}{8} \right)^{2} \right] = 0,429.\)

Logo, os índices Gini calculados foram:

gini = tibble("Variáveis" = c("Outlook = Overcast", "Outlook = Rain", "Outlook = Sunny", "Humidity = High", "Wind = Strong"), "Índice Gini" = c("0,357", "0,457", "0,394", "0,367", "0,429"))

knitr::kable(gini)

Selecionamos a variável com o menor índice Gini para ser o primeiro toco da floresta. Nesse caso, o menor índice Gini é o da variável “Outlook = Overcast”.

Agora precisamos calcular o peso desse toco na classificação final. Para isso, vamos calcular seu erro total.

O erro total de um toco é calculado pelo número de amostras classificadas erradas dividido pelo total de amostras.

Para esse toco houve 5 amostras classificadas erradas em um total de 14. Logo,

\[ \hbox{Erro Total} = \frac{5}{14}. \]

Dessa forma podemos calcular o Amount of Say do toco, que será seu peso na classificação final.

\[ \hbox{Amount of Say} = \frac{1}{2} \times log \left( \frac{1-\hbox{Erro Total}}{\hbox{Erro Total}} \right) \] Logo, o Amount of Say desse toco será de:

\[ \hbox{Amount of Say} = \frac{1}{2} \times log \left( \frac{1-5/14}{5/14} \right) = 0,29.\]

Então 0,29 é o seu peso na classificação final.

Agora vamos construir o próximo toco. Para isso damos um peso maior para as amostras que foram classificadas erroneamente no toco anterior. Essas amostras foram as seguintes:

golf %>% filter(Outlook != "Overcast" & Play != "No")

Então, para rebalancearmos os pesos das amostras classificadas de forma certa e errada, utilizamos as seguintes fórmulas:

\[ \hbox{Peso Amostras Erradas} = \hbox{Erro Total} \ \times e^{\hbox{Amount of Say}}\] \[ \hbox{Peso Amostras Corretas} = \hbox{Erro Total} \ \times e^{-\hbox{Amount of Say}}\]

Assim, para o segundo toco, os pesos serão:

\[ \hbox{Peso Amostras Erradas} = \frac{5}{14} \ \times e^{0,29} = 0,477.\] \[ \hbox{Peso Amostras Corretas} = \frac{5}{14} \ \times e^{-0,29} = 0,267.\]

Então temos os pesos para as amostras:

A soma dos pesos das amostras deve ser 1, mas isso não ocorre: note que a soma resulta em 4,788. Dessa forma, precisamos reescalar os pesos. Faremos isso dividindo cada um deles por 4,788.

Feito isso, temos uma nova tabela de pesos:

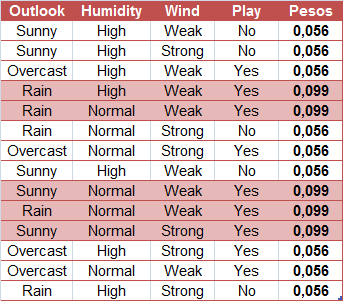
Definidos os pesos, em seguida realizamos uma reamostragem via bootstrap (uma amostragem da própria amostra, com reposição) do mesmo tamanho da base de dados original. A probabilidade de um elemento da amostra ser sorteado é o peso dele.

# Numerando os elementos da amostra:
amostra = 1:14

# Definindo as probabilidades dos elementos serem sorteados:
pesos = rep(c(0.056, 0.099, 0.056, 0.099, 0.056), times = c(3,2,3,3,3))

# Realizando o bootstrap:
set.seed(271)
sample(amostra, size = 14, replace = T, prob = pesos)

Então temos uma nova amostra formada pelos elementos sorteados na reamostragem:

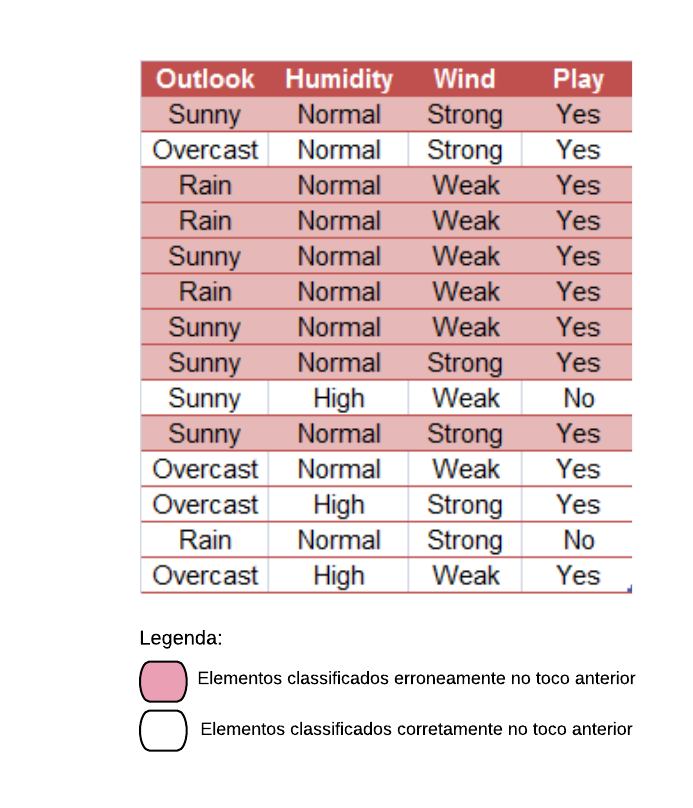
Agora, com essa nova amostra, fixamos pesos uniformes para os elementos e repetimos o processo de criação para o próximo toco. Em seguida verificamos os elementos que foram classificados de forma errada, aumentamos seus pesos no banco de dados e repetimos o processo de bootstrap, construindo, assim, o próximo toco. O processo se repete até que a floresta de tocos esteja concluída.

Finalizada a floresta, realizamos a classificação final dos elementos somando os pesos dos tocos para cada classificação e selecionando o maior deles. Por exemplo, em uma floresta com 10 árvores onde 5 delas classificam a amostra na categoria de interesse como “positivo” e 5 delas classificam essa mesma amostra como “negativo”, se a soma dos pesos das que classificaram a amostra como “positivo” for 2,7 e a das que classificaram a amostra como “negativo” for 0,84, a amostra será classificada como “positivo”.

Adaboost com o train

Agora que já sabemos como funciona o adaboost, vamos botá-lo em prática através da função train(). Para isso basta escolhermos essa opção no argumento referente ao método de treino que será utilizado. Vamos fazer isso utilizando a base de dados College, utilizando o mesmo conjunto treino e teste utilizado no exemplo de árvores de decisão, para compararmos os resultados.

college = readr::read_csv2("College.csv")

# Separando a amostra em treino e teste:
set.seed(100)
noTreino = caret::createDataPartition(y = college$Private, p = 0.7, list = F)
treino = college[noTreino,]
teste = college[-noTreino,]

# Treinando o modelo com o adaboost:
modelo = caret::train(Private~., method = "adaboost", data = treino)
modelo

Vamos aplicar o modelo no conjunto teste e avaliá-lo através da matriz de confusão.

predicao = predict(modelo, teste)

# Transformando em fator para depois construirmos a matriz de confusão:
teste$Private = as.factor(teste$Private)

# Construindo a matriz de confusão:
confusionMatrix(predicao, teste$Private)

Note que obtivemos resultados melhores utilizando o adaboost do que simplesmente uma árvore de decisão. A acurácia, em particular, subiu de 0,89 para 0,92.

Adaboost com o pacote adabag

Também podemos utilizar o pacote adabag para treinarmos um modelo pelo adaboost. Vamos utilizar a base de dados spam.

Inicialmente vamos separar a amostra em treino e teste.

library(kernlab)
data(spam)
set.seed(16)
noTreino = createDataPartition(y = spam$type, p = 0.7, list = F)
treino = spam[noTreino,]
teste = spam[-noTreino,]

Antes de realizarmos o adaboost precisamos definir a profundidade máxima que as árvores da floresta terão. Faremos isso através do comando rpart.control(). Como o objetivo é construir uma floresta de tocos, as árvores terão todas profundidade 1.

library(rpart)
controle = rpart.control(maxdepth = 1)

Agora vamos aplicar o método adaboost no conjunto treino utilizando o comando boosting().

library(adabag)
modelo = boosting(formula = type~., data = treino, boos = T, mfinal = 100,
                  coeflearn = "Breiman", control = controle)

Os principais argumentos dessa função são:

• formula = uma fórmula especificando qual variável queremos prever em função de qual(is);
• data = base de dados onde se encontram as variáveis;
• boos = argumento do tipo logical onde, se TRUE (default), utiliza bootstrap para criar uma nova amostra treino para a próxima árvore baseado nos erros da árvore anterior;
• mfinal = número de árvores da floresta;
• coeflearn = define qual fórmula será utilizada para o Amount of Say de cada árvore. A que vimos é a fórmula de Breiman (default);
• control = opções que controlam detalhes do algoritmo rpart.

Para visualizarmos qualquer árvore da floresta utilizamos o comando rpart.plot().

library(rpart.plot)

# Visualizando a primeira árvore construída:
rpart.plot(modelo$trees[[1]])

Por último, vamos aplicar o modelo na amostra teste e em seguida avaliar o modelo através da matriz de confusão.

predicao = predict(modelo, teste)

# Resumo da matriz de confusão:
predicao$confusion

---

Gradiente Boosting

em Regressão

De acordo com Jerome Friedman, o criador do Gradiente Boosting, evidências empíricas mostram que dar pequenos passos ou ir gradativamente na direção correta resulta em melhores predições na amostra teste, ou seja, menor variância.

Para entendermos como funciona o Gradiente Boosting, considere a seguinte base de dados.

base = readr::read_csv("peso.csv")
base

A primeira coisa a fazer é definir um número máximo de folhas de cada árvore. Para nosso exemplo, vamos definir 4 folhas, mas em geral, é definido uma quantidade de 8 a 32 folhas. Feito isso, tiramos uma média dos pesos dos indivíduos e essa será nossa primeira árvore, uma árvore só com a raiz.

{width=30%}

Agora, calculamos o Pseudo-Resíduo, o erro de previsão de cada indivíduo, da forma \[Pseudo\ Resíduo = valor\ real – valor\ predito\] para cada observação. Então, por exemplo, o pseudo-resíduo da primeira observação vai ficar \(88-71.5 = 16.5\) .

base1 = readr::read_csv("peso1.csv")
base1

O termo pseudo-resíduo é baseado em Regressão Linear, onde o resíduo é a diferença entre os valores observados e estimados. O termo “pseudo” serve para lembrar que estamos fazendo Gradiente Boosting e não Regressão Linear.

O próximo passo é, utilizando as variáveis explicativas (Altura, Cor e Sexo), construir uma árvore de decisão respeitando o máximo de folhas definido anteriormente. Mas ela deve predizer o pseudo-resíduo e não o Peso.

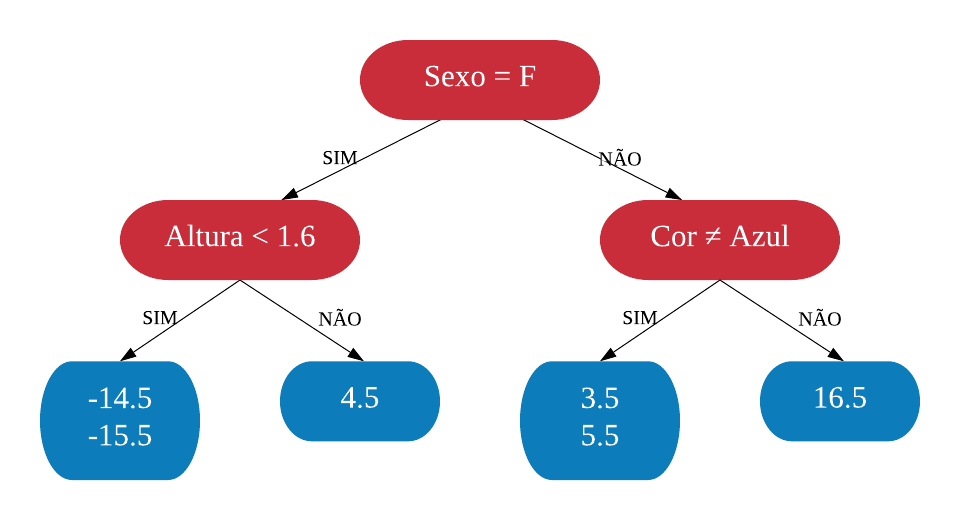
{width=85%}

Note que temos mais observações do que folhas, sendo assim, podemos ter mais que um resultado em cada uma. Nesse caso, substituímos os valores pela média das folhas.

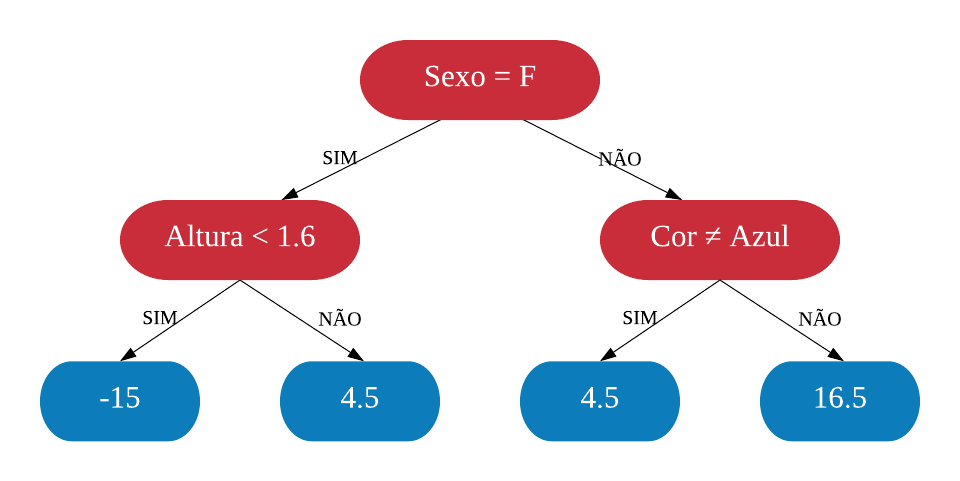
{width=85%}

Agora somamos o resultado das duas árvores para classificar na primeira observação, por exemplo, a predição seria \(71.5+16.5=88\). Acertamos exatamente o valor real. Isso é bom? Não. Já vimos como não é bom ter um modelo muito ajustado. Temos pouco viés, mas provavelmente alta variância.

O Gradiente Boosting lida com esse problema usando uma taxa de aprendizado para reescalar a contribuição da nova árvore. A taxa de aprendizado é um número entre 0 e 1 e deve ser multiplicado ao valor da segunda árvore em diante. Para esse exemplo, vamos adotar uma taxa de 0.1, assim a predição da primeira observação seria \(71.5+(0.1*16.5)=73.15\) . A predição não ficou tão boa, mas é um pouco melhor do que o resultado de apenas uma árvore.

Feito isso, recalculamos os valores do pseudo-resíduo.

base2 = readr::read_csv("peso2.csv")
base2

Repare que o valor do segundo pseudo-resíduo diminuiu em módulo em relação ao primeiro, ou seja, nos aproximamos mais do valor correto do que da primeira vez.

Agora, utilizando novamente as variáveis explicativas, construímos outra árvore agora para predizer o segundo pseudo-resíduo.

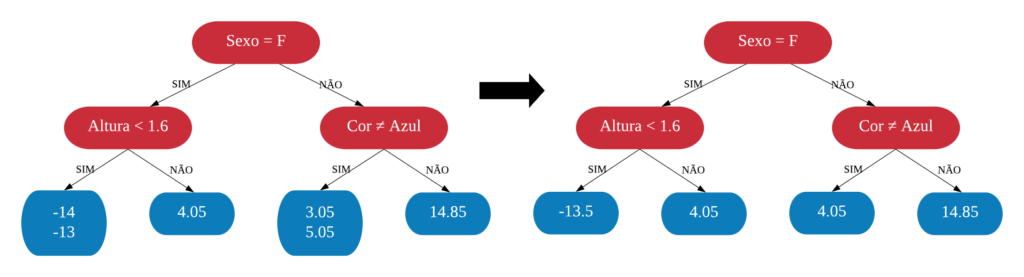
{width=100%}

Note que a estrutura da segunda árvore construída ficou semelhante a primeira. Isso não acontece sempre, mas pode acontecer.

Agora, a classificação da primeira observação ficaria \(71.5+(0.1*16.5)+(0.1*14.85)=74.635\) um pouco mais perto do verdadeiro valor. Repetimos esse procedimento quantas vezes se queira ou até não ter redução significante dos valores do pseudo-resíduo. Dessa forma temos uma sequência de árvores que caminham em direção ao valor correto em passos pequenos.

É importante notar que todas as árvores devem possuir a mesma taxa de aprendizado.

Construindo um regressor com o pacote gbm

Para nosso exemplo, vamos utilizar a base de dados Wage do pacote ISLR. Para isso, vamos precisar limpar os dados removendo variáveis de variância zero.

# lendo a base de dados
library(ISLR)
data("Wage")
# removendo variaveis de variancia zero
vvz = nearZeroVar(Wage,saveMetrics = F)
vvz
Wage = Wage[,-vvz]

Dividimos a base nos conjuntos de treino e teste.

set.seed(100)
noTreino = createDataPartition(Wage$wage,p=0.7,list=F)
treino = Wage[noTreino,]
teste = Wage[-noTreino,]

Agora vamos aplicar o gradiente boosting com a função gbm()

library(gbm)
modelo = gbm(wage~.,data=treino, distribution="gaussian",
              n.trees =300,interaction.depth = 20)
modelo

Os principais argumentos da função gbm() são:

• distribution: gaussian se for regressão, multinomial se for um classificação, bernoulli se for classificação 0-1.
• n.trees: número de árvores da floresta.
• interaction.depth: profundidade máxima das árvores.

Vamos aplicar o modelo na amostra teste, e avaliar o resultado.

predicao = predict(modelo, teste, n.trees=300)
# avaliando
postResample(predicao,teste$wage)

Note que utilizamos 300 árvores. Mas pode ser que não seja necessário essa quantidade de árvores pra alcançar esses valores de \(R^2\), RMSE e MAE. Para saber a quantidade ideal de árvores, isto é, quando erro se estabiliza, podemos utilizar a função gbm.perf().

gbm.perf(modelo)

Sendo assim, com apenas 50 árvores teríamos chegado a um resultado razoável.

predicao2 = predict(modelo, teste, n.trees=50)
postResample(predicao2,teste$wage)

em Classificação

Considere a seguinte base de dados

base = readr::read_csv("Troll 2.csv")
base

Queremos predizer se uma pessoa ama o filme Troll 2 baseado em seu gosto por pipoca, idade e cor favorita. Assim como em regressão, começamos o método de Gradiente Boosting usando uma árvore raiz que represente nossa predição inicial para cada observação. Em regressão usamos a média das observações, em classificação vamos usar o log(chances). Olhando na base de dados, podemos dizer que as chances de alguém amar Troll 2 é \[chances= \frac{Quantidade\ de\ indivíduos\ que\ amaram}{Quantidade\ de\ indivíduos\ que\ odiaram} = \frac{4}{2}\] portanto, o \(log(chances)=log(\frac{4}{2}) = 0.6932\) e é isso que colocaremos na folha inicial.

{width=30%}

Assim como em regressão logística, o jeito mais fácil de usar o log(chances) para classificar é convertendo em probabilidade, e fazemos isso usando a seguinte função logística \[ Probabilidade = \frac{e^{log(chances)}}{1+e^{log(chances)}}\] Sendo assim, A \(Probabilidade\ de\ alguém\ amar\ Troll2 = \frac{e^{log(\frac{4}{2})}}{1+e^{log(\frac{4}{2})}} = \frac{2}{3}=0.6667\).

{width=30%}

É importante notar que o log(chances) e a probabilidade só ficaram iguais por causa da aproximação.

Podemos usar um limite de corte 0.5, sendo assim, já que a probabilidade ficou maior que o corte, nós classificamos todos no treino como indivíduos que amam Troll 2.

Embora 0.5 seja um limite usual para tomada de decisão baseada em probabilidade, poderiamos tranquilamente usar um valor diferente.

Mas a classificação não ficou muito boa já que 2 indivíduos foram classificados erroneamente. Podemos mensurar quão ruim foi a predição calculando o \(pseudo\ resíduo = observado – predito\). Para essa conta, perceba que se um indivíduo ama Troll 2, então a probabilidade dele amar Troll 2 é 1. Semelhantemente, se ele odeia, a probabilidade dele amar é 0. Assim, calculamos os pseudo-resíduos.

base = readr::read_csv("Troll2 1.csv")
base

Agora, construímos uma árvore utilizando as variáveis explicativas para predizer o pseudo-resíduo. Assim como o Gradiente Boosting para regressão, temos que definir um número máximo de folhas em cada árvore. Aqui vamos limitar a 3 folhas, mas na prática geralmente é um número entre 8 e 32.

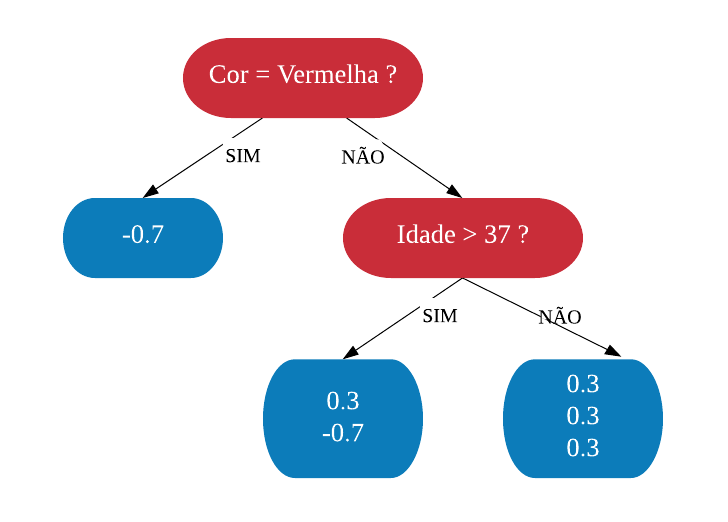
{width=80%}

Em regressão, os valores das folhas representavam os resíduos. Mas em classificação isso é mais complexo. Isso porque a predição está em log(chances) e as folhas são provenientes de probabilidade. Portanto não podemos apenas soma-las para uma nova predição sem alguma transformação. A transformação mais comum por folha é \[\frac{\sum resíduos}{\sum[prob.\ anterior * (1-prob.\ anterior)]}\]

Assim, da esquerda pra direita, para primeira folha temos \[\frac{\sum resíduos}{\sum[prob.\ anterior * (1-prob.\ anterior)]}=\frac{-0.7}{0.7*(1-0.7)}=-3.3333\], para a segunda \[\frac{\sum resíduos}{\sum[prob.\ anterior * (1-prob.\ anterior)]}=\frac{0.3+(-0.7)}{(0.7*(1-0.7))+(0.7*(1-0.7))}=-0.9524\] e para última \[\frac{\sum resíduos}{\sum[prob.\ anterior * (1-prob.\ anterior)]}=\] \[\frac{0.3+0.3+0.3}{(0.7*(1-0.7))+(0.7*(1-0.7))+(0.7*(1-0.7))}=\frac{3*0.3}{3*(0.7*(1-0.7))}=1.4286\]

Por enquanto, a probabilidade anterior é a mesma para todos, mas a partir da próxima árvore isso muda.

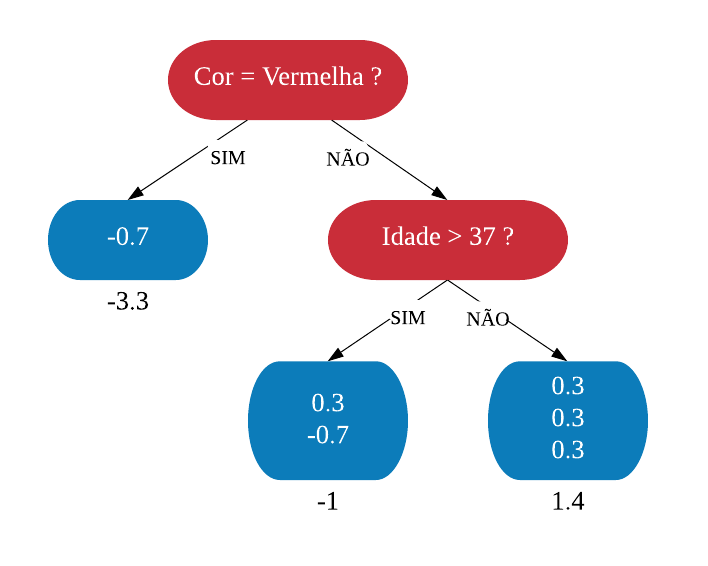
{width=80%}

Agora que todas as folhas foram alteradas, podemos somar os resultados escalados pela taxa de aprendizado. Nesse exemplo, vamos usar uma taxa alta, 0.8. Mas geralmente se usa 0.1. E então calculamos o novo \(log(chances)=log(chances)\ anterior + taxa\ de\ aprendizado * log(chances)\ obtido\ na\ árvore\). Para primeira observação, por exemplo, fica \(log(chances)=0.7+(0.8*1.4)=1.82\) e então convertemos em probabilidade \(\frac{e^{1.82}}{1+e^{1.82}} = 0.8606\). Então, note que fizemos progresso, já que o indivíduo em questão ama Troll 2. Antes ele foi classificado corretamente mas com probabilidade 0.7, agora ele foi classificado corretamente mas com probabilidade 0.9.

base = readr::read_csv("Troll2 2.csv")
base

Pode ser que a previsão fique pior, como no caso do segundo indivíduo. E essa é a razão de construírmos várias árvores e não só uma.

Calculamos os novos pseudo-resíduos que agora serão diferentes para cada observação.

base = readr::read_csv("Troll2 3.csv")
base[,-5]

Construímos uma segunda árvore agora para prever os novos pseudo-resíduos e fazemos a transformação para log(chances) para cada folha.

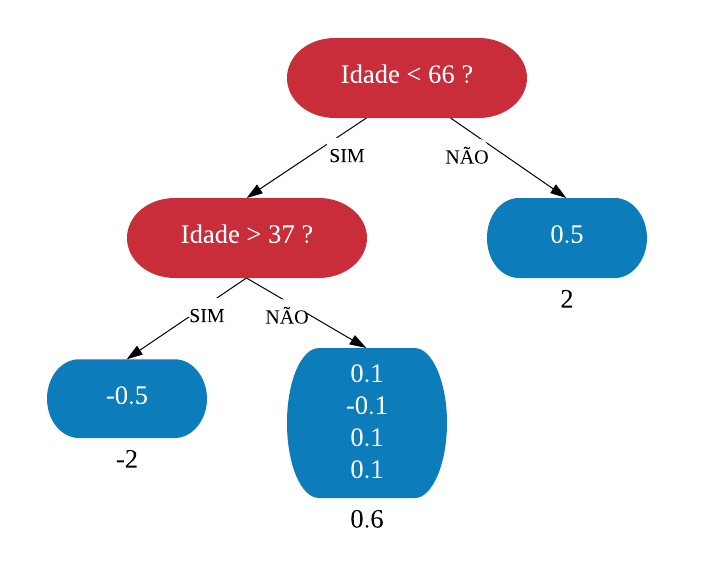
{width=80%}

Combinamos com as árvores anteriores para obter um valor de saída e transformamos em Probabilidade para classificar. Por exemplo, a primeira observação ficaria \(log(chances)=0.7+(0.8*1.4)+(0.8*0.6)=2.3\) e então convertemos em probabilidade \(\frac{e^{1.82}}{1+e^{1.82}} = 0.9089\). Dessa forma, continuamos construíndo quantas árvores forem necessárias.

Construindo um classificador com o pacote gbm

O gradiente boosting para classificação no R é semelhante ao para regressão, atentando para o argumento distribution, que deve ser igual a “bernoulli” se a variável de interesse tiver apenas duas respostas possíveis (como no caso da bse Troll 2) ou “multinomial” se a variável tiver mais de duas respostas possíveis. Por exemplo, considere a base Vehicle do pacote mlbench. Nela, estamos interessados em classificar a variável Class, que pode ser bus, opel, saab ou van.

# lendo a base
library(mlbench)
data(Vehicle)
# dividindo em treino e teste
library(caret)
set.seed(100)
noTreino = createDataPartition(Vehicle$Class,p=0.7,list=F)
treino = Vehicle[noTreino,]
teste = Vehicle[-noTreino,]
# treinando o modelo
library(gbm)
modelo = gbm(Class~.,data=treino,distribution="multinomial",
              n.trees = 100,interaction.depth = 8)

Quando aplicamos o predict(), o que recebemos de retorno são um conjunto de probabilidades (ou o log(chances)), e não a classificação final. Cabendo ao pesquisador definir a regra de classificação final.

predicao = predict(modelo, teste, n.trees=100, type = 'response')

O argumento ´type´ retorna por default o log(chances), se definimos como “response” ele retorna a probabilidade.

# Criando a regra de classificacao
k = dim(teste)[1]
classe = c()
for (i in 1:k){
  classe[i] = names(which.max(predicao[i,1:4,1])) 
}
head(classe)
# verificando quantidade de arvores necessarias
gbm.perf(modelo)
# avaliando o modelo 
confusionMatrix(data=as.factor(classe), reference=as.factor(teste$Class))

---

XGBoost {#link10}

O XGBoost é a abreviação de Extreme Gradient Boost. Ele foi desenvolvido para suportar um grande volume de dados de forma eficiente. Geralmente é 10 vezes mais rápido que o Gradiente Boosting.

Em Regressão

Apesar do XGBoost ser usado para lidar com bases grandes, vamos usar uma base de dados bem pequena só para entendermos melhor como ele funciona. Queremos predizer o peso de um indivíduo em função de sua altura.

# lendo e vizualizando a base
library(readr)
(peso = read_csv("peso-altura.csv"))
library(ggplot2)
ggplot(peso, aes(x=Altura, y=Peso)) + geom_point(lwd=5, colour = "deeppink3") + 
  theme_minimal() + ylim(c(50,90)) + xlim(c(1.3,1.9))

****************** O primeiro passo é fazer uma predição inicial que pode ser qualquer uma. O defaut é usar 0.5, mas como estamos falando de peso, vamos utilizar a predição inicial “Peso = 70”.

{width=80%}

Agora precisamos calcular os resíduos (diferença entre o valor real e o valor predito) que vão nos mostrar quão boa é essa predição.

library(dplyr)
(peso = peso %>% mutate( residuos = Peso-70 ))

Assim como no Gradiente Boosting, o próximo passo é construir uma árvore para predizer os resíduos. Mas o XGBoost utiliza uma árvore de regressão diferente que vamos chamar de árvore XGB. Existem muitas formas de construir uma árvore XGB. Vamos aprender a mais comum. A árvore XGB inicia com uma folha que leva todos os resíduos.

{width=80%}

Em seguida, calculamos um índice de qualidade ou Índice de similaridade \[Índice\ Similaridade\ = \frac{(soma\ dos\ resíduos)^2}{número\ de\ resíduos + \lambda} \] Onde \(\lambda\) (lambda) é um parâmetro de regularização, o que significa que tem o objetivo de reduzir a sensibilidade das observações individuais, ou seja, reduzir o sobreajuste. Por enquanto, vamos considerar \(\lambda = 0\) porque esse é o valor default. Sendo assim, o Índice de similaridade da raiz é \(\frac{(18+6-14+5-10)^2}{5+0}=\frac{5^2}{5}=5\)

{width=80%}

Agora vamos ver se conseguimos melhorar esse índice dividindo os resíduos, ou seja, criando uma ramificação. Vamos começar dividindo a variável Altura na média entre os dois menores valores, que são \(1.4\) e \(1.5\), e calculando o Indice para as novas folhas.

Observe que nas folhas não estarão as alturas e sim os resíduos correspondentes a altura especificada.

<img src="http://cienciadedados.uff.br/wp-content/uploads/sites/195/2020/04/image-31.png" alt="Figura 4: Dividindo por 'Altura

{width=80%}

Agora, precisamos calcular o ganho dessa ramificação para ver o quanto ela foi efetiva. O ganho é calculado da seguinte forma: \[ganho = IS_{folha\ da\ esquerda} + IS_{folha\ da\ direita} – IS_{raiz}\] Assim, o ganho da ramificação ‘Altura<1.45’ é \(100 + 56.25 – 5 = 151.25\). Vamos fazer esse calculo em todas as ramificações possiveis, Isto é, se temos 5 observações com diferentes alturas, vamos ter 4 ramificações possiveis: ‘Altura<1.45’, ‘Altura<1.55’, ‘Altura<1.65’ e ‘Altura<1.75’.

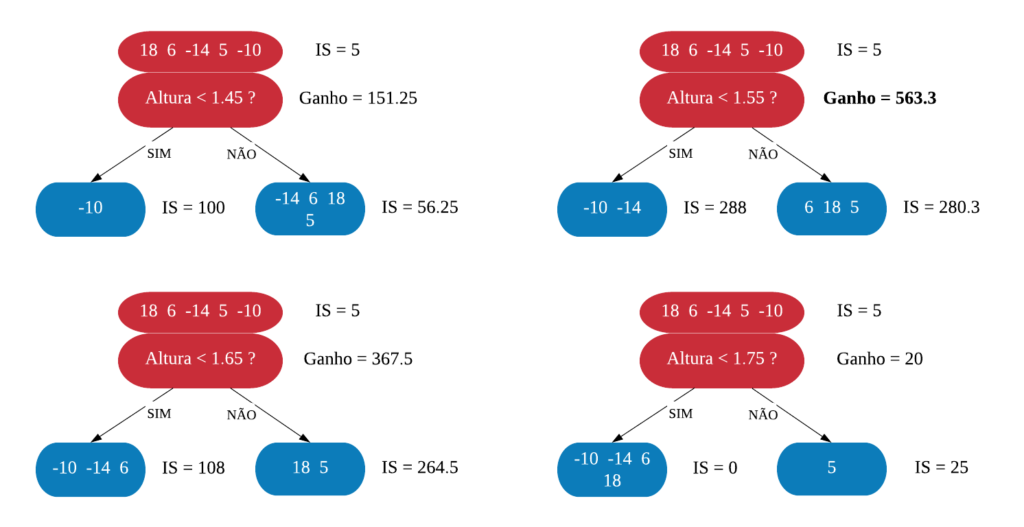
{width=100%}

Podemos ver que o ganho de usar a ramificação ‘Altura<1.55’ é maior, portanto é essa que vamos usar. Agora vamos ramificar as folhas da mesma maneira e escolher as que tiverem melhor ganho.

Nesse exemplo, vamos limitar a profundidade da árvore XGB em 2. Mas o default é permitir até 6 níveis de profundidade.

Nossa árvore XGB final ficou:

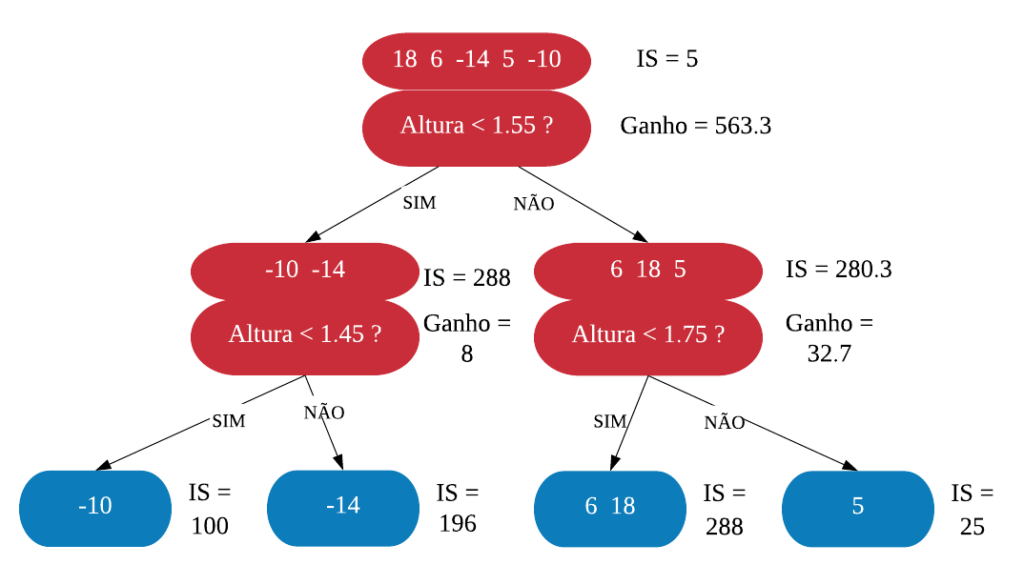
{width=80%}

Agora, vamos podar nossa árvore. Fazemos isso porque pode ser que algum nó tenha o ganho muito baixo e por isso não vale a pena estar na árvore. Para decidir se vamos tirar algum nó e, se sim, qual, vamos escolher um valor que será chamado de \(\gamma\) (gamma). Em seguida, calculamos a diferença entre o ganho associado ao nó e \(\gamma\), se essa diferença for negativa, então removemos o nó.

\(\gamma\) especifica o ganho mínimo necessario para fazer uma divisão. Seu default é 0. Quanto maior, mais conservador é o modelo.

Mesmo quando \(\gamma = 0\) isso não previne podas.

Vamos escolher \(\gamma = 10\). Começando sempre dos nós mais profundo para a raiz, vamos avaliar a diferença entre o ganho e \(\gamma\). No nó mais a direita, temos que o ganho é 32.7, portanto a diferença é \(32.7-10=22.7\) como o resultado é positivo, o nó permanece. No nó a esquerda, a diferença fica \(8-10=-2\), como o resultado é positivo, retiramos esse nó. Assim, estamos dizendo que o ganho do nó à esquerda não é bom o suficiente pra justificar essa ramificação. Como o nó à direita permaneceu na árvore, não faz sentido calcular essa diferença para o nó raiz.

Mesmo se o valor da diferença der negativo nos nós de cima, se não removermos o de baixo, o de cima não é removido.

Com isso, nossa árvore XGB ficou:

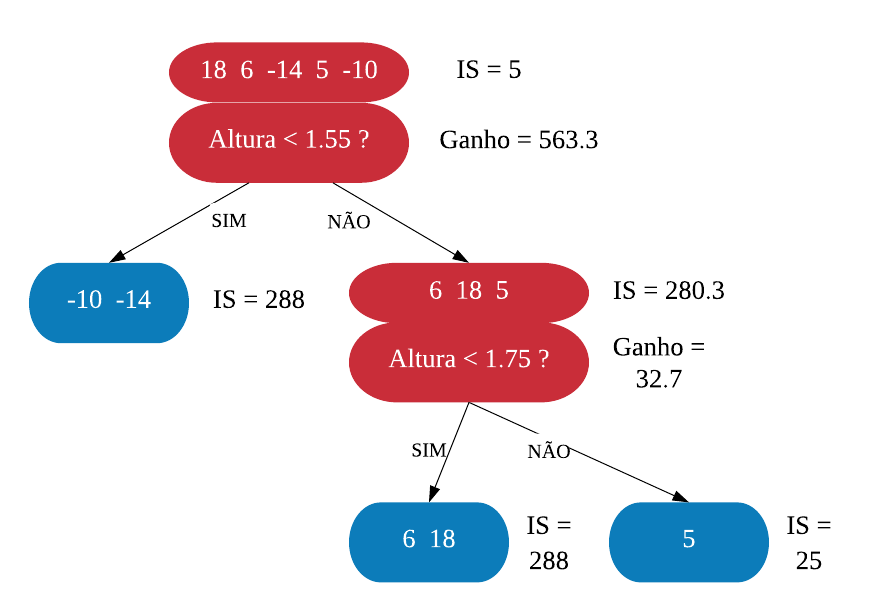
{width=80%}

Note que se tivéssemos escolhido um \(\gamma\) muito alto, por exemplo \(\gamma = 570\), toda árvore seria podada. É preciso cuidado.

Agora vamos voltar ao inicio e reconstruir a árvore agora usando \(\lambda = 1\) (lembra do \(\lambda\)? aquele da fórmula do índicador de similaridade 🙂 ). Para facilitar a vizualização, vamos omitir os cálculos. A nova árvore XGB ficou:

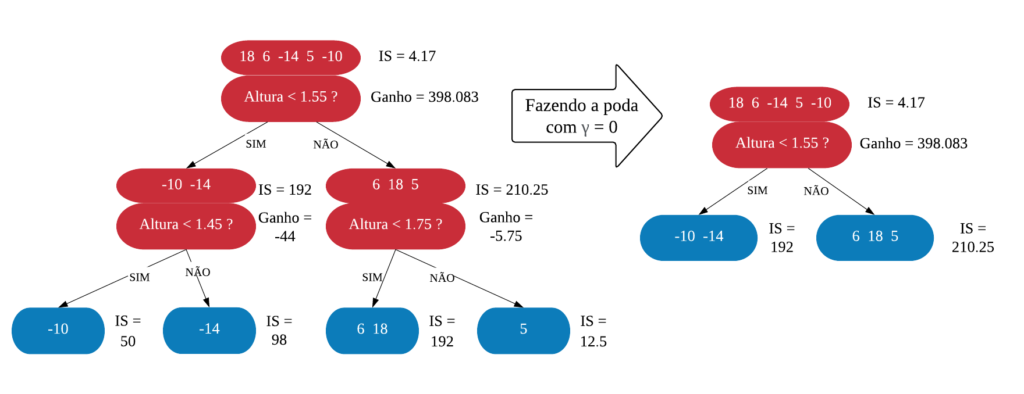
{width=100%}

Podemos notar que quando \(\lambda > 0\), o índice de similaridade é menor. O que significa que se mantivermos o mesmo \(\gamma\), a poda será mais extrema. Por outro lado, deixar \(\lambda > 0\) ajuda a previnir sobreajustes.

Agora que temos árvore final, vamos calcular os valores de saída das folhas. \[valores\ de\ saida = \frac{soma\ dos\ residuos}{número\ de\ resíduos + \lambda}\] Repare que essa fórmula é bem parecida com a do índice de similaridade, mas a soma dos resíduos não está ao quadrado.

Repare que, como \(\lambda = 0\) o valor de saida é uma média aritmética simples entre os resíduos. Mas note que se \(\lambda > 0\) e a folha tiver apenas uma observação, isso reduzira a sensibilidade dessa observação individual evitando sobreajuste.

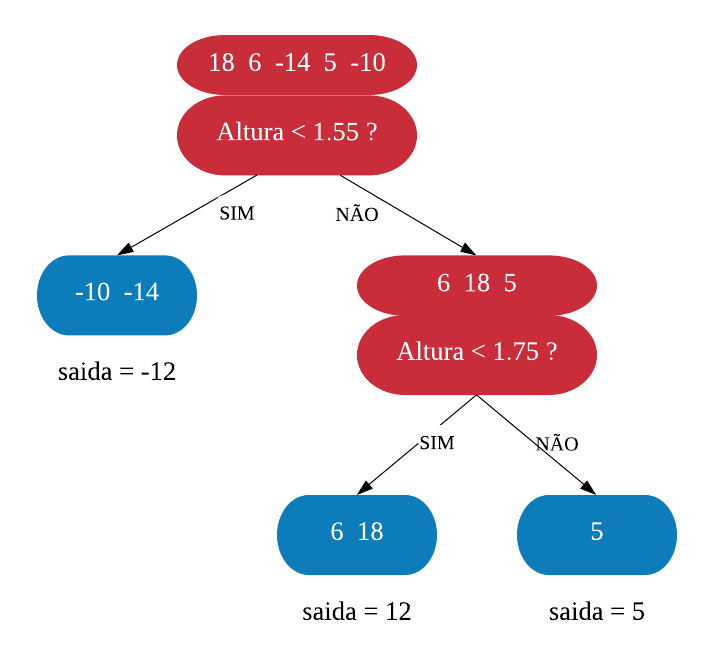
{width=80%}

Assim a primeira árvore está completa e, como em Gradient Boosting, fazemos novas predições começando com a predição inicial e somando com o resultado da árvore XGB escalada pela taxa de aprendizado.

O XGBoost chama a taxa de aprendizado de \(\varepsilon\) (eta) e seu valor default é 0.3, que é o que vamos usar.

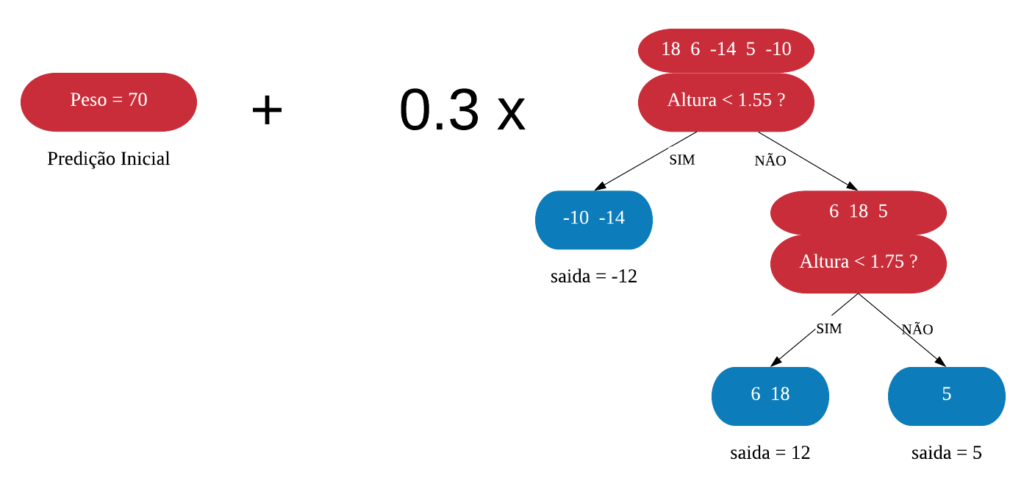
{width=80%}

Por exemplo, se a gente pegasse a primeira observação (indivíduo com altura=1.7), seu peso predito seria \(predicao\ inicial + \varepsilon*valor\ de\ saida\ da \ árvore\ XGB = 70+0.3*12=73.6\) que é mais perto do seu peso real (que era 88) do que a predição anterior (70). Assim, com as novas predições, os novos resíduos ficaram:

nova_pred = c(73.6, 73.6, 66.4, 71.5, 66.4)
(peso = peso %>% mutate( residuos2 = Peso - nova_pred ))

Perceba que o novo resíduo é melhor que o anterior (seu valor absoluto é mais próximo de 0). Ou seja, estamos dando pequenos passos na direção correta.

Agora construímos outra árvore XGB da mesma forma, mas para predizer os novos resíduos, Dessa forma obteremos previsões com resíduos menores. E continuamos construíndo árvores XGB até que os resíduos sejam bem pequenos ou até atingir o número de árvores desejado.

Em Classificação

Para entendermos como o XGBoost funciona para problemas de classificação, vamos utilizar a base de dados a seguir. O objetivo é prever se a universidade é pública ou privada baseado nos pedidos para ingresso.

OBS: Assim como comentado anteriormente em regressão, o XGBoost foi projetado para bases de dados grandes, mas para fins didáticos iremos utilizar uma base bem pequena.

library(readxl)
college = read_excel("SmallCollege.xlsx")
college

library(ggplot2)
library(dplyr)
college %>% ggplot(aes(x = Apps, y = Private)) + geom_point(lwd = 5, aes(colour = Private)) +
  guides(col = F) + theme_minimal()

O primeiro passo é fazer uma predição inicial. Essa predição pode ser qualquer valor, como por exemplo a probabilidade de observar universidades públicas no conjunto de dados. Por default, essa predição é de 0,5.

Podemos ilustrar essa predição inicial adicionando uma linha horizontal no gráfico que representa as probabilidades de uma universidade ser pública pelo que observamos no conjunto de dados.

college$Probabilidade = ifelse(college$Private == "Yes", 0, 1)
college %>% ggplot(aes(x = Apps, y = Probabilidade)) + 
  geom_point(lwd = 5, aes(colour = Private)) + theme_minimal() + 
  ylab("Probabilidade da Universidade ser Pública") + geom_hline(yintercept = 0.5, type = 2)

Feita a predição inicial, agora vamos calcular os resíduos e verificar quão boa é essa predição.

college$Residuos = college$Probabilidade-0.5
college

O próximo passo é construir uma árvore para predizer os resíduos. Assim como a árvore XGB para regressão, a árvore XGB para classificação se inicia com apenas uma folha que leva todos os resíduos.

Agora precisamos calcular o Índice de Similaridade para os resíduos. Porém, como estamos usando XGBoost para classificação, temos uma nova fórmula para ele.

\[ \hbox{Índice de Similaridade} = \frac{\left( \sum\limits_{i=1}^{n} \hbox{Resíduo}_i \right)^{2}}{\sum\limits_{i=1}^{n} \left[ \hbox{Probabilidade Prévia}_i \times \left( 1 – \hbox{Probabilidade Prévia}_i \right) \right] + \lambda} \]

Veja que o numerador da fórmula para classificação é igual ao da fórmula para regressão. E assim como para regressão, o denominador contém \(\lambda\), o parâmetro de regularização.

Note que o numerador do Índice de Similaridade para a folha resultará em 0, pois nós somamos os resíduos antes de elevá-los ao quadrado, o que faz com que eles se cancelem.

\[\left( \sum\limits_{i=1}^{n} \hbox{Resíduo}_i \right)^{2} = (0,5 – 0,5 – 0,5 + 0,5)^{2} = 0 \Rightarrow \hbox{Índice de Similaridade} = 0\]

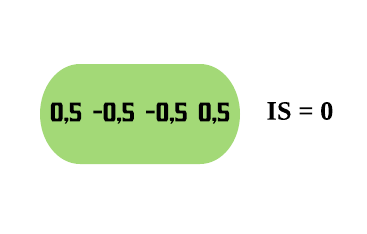
Vamos tentar melhorar o Índice dividindo os resíduos em 2 grupos diferentes.

Construindo um regressor com o pacote xgboost

Em Classificação

Vamos usar a base de dados winequality-red. O objetivo dessa base é prever a qualidade do vinho baseado em suas outras variáveis. Mas nós vamos tentar prever o nível alcoólico do vinho.

library(readr)
wine = read_csv2("winequality-red.csv")
str(wine)

Como sempre, vamos dividir a base em amostra de treino e amostra de teste.

library(caret)
set.seed(100)
noTreino = createDataPartition(wine$alcohol ,p=0.7,list=F)
# vendo a classe da base de dados
class(wine)

O pacote xgboost só le matrizes. Então teremos que transformar a base numa matriz. Além disso, teremos que separar a váriavel de interesse das variáveis explicativas.

# Transformando a base em matriz
wine = as.matrix(wine)
class(wine)
# separando amostra treino e teste
treino       = wine[noTreino,-11] # a variável 'alcohol' é a 11ª coluna
treino_label = wine[noTreino, 11]

teste       = wine[-noTreino,-11]
teste_label = wine[-noTreino, 11]

Agora, podemos usar a função xgboost para criar nosso modelo.

library(xgboost)
modelo = xgboost(data = treino, label = treino_label,
                 gamma=0, eta=0.3, 
                 nrounds = 100, objective = "reg:squarederror")

predicao = predict(modelo,teste)
mse = sum((teste_label-predicao)^2)/length(predicao)

---

Referências

JAMES, G. et al. An Introduction to Statistical Learning: with applications in R. New York: Springer, 2013.

HASTIE, T.; TIBSHIRANI, R.; FRIEDMAN, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction. Stanford: Springer, 2008.

PRACTICAL Machine Learning. Coursera. Disponível em https://www.coursera.org/learn/practical-machine-learning. Acesso em 2019.

STARMER, Josh. Machine Learning, 2018. Disponível em https://www.youtube.com/watch?v=Gv9_4yMHFhI&list=PLblh5JKOoLUICTaGLRoHQDuF_7q2GfuJF. Acesso em 2019.

R Core Team (2019). R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. URL https://www.R-project.org/.

---

Apêndice{#link9}

Outras Medidas da Matriz de Confusão

No capítulo de avaliação de preditores introduzimos a matriz de confusão e as medidas de avaliação mais utilizadas: sensibilidade, especificidade e precisão. Vimos também como construí-la de forma rápida e prática com a função confusionMatrix() do pacote caret. Porém, além das 3 medidas mais utilizadas, a função também libera algumas outras, que explicaremos como elas são calculadas a seguir.

Vamos ver a saída da função para o mesmo exemplo dado anteriormente, onde utilizamos a base de dados spam. Nesse exemplo nós treinamos o modelo pelo método GLM e em seguida aplicamos ele ao conjunto teste. Avaliamos o modelo utilizando a matriz de confusão gerada pela função confusionMatrix().

library(caret)
library(kernlab)
data(spam)
set.seed(371)
noTreino = createDataPartition(y = spam$type, p = 0.75, list = F)
treino = spam[noTreino,]
teste = spam[-noTreino,]
modelo = caret::train(type ~ ., data = treino, method = "glm")
predicao = predict(modelo, newdata = teste)
confusionMatrix(predicao, teste$type)

Além de Accuracy (Precisão), Sensitivity (Sensibilidade) e Specificity (Especificidade), as outras saídas representam o seguinte:

• 95% CI = intervalo de confiança com 95% de confiança para a precisão;
• No Information Rate (Taxa de Não-Informação) = a maior proporção estimada de classe nos dados. Nesse exemplo a taxa foi de 0,6061, o que significa que aproximadamente 60% dos dados são “não spam”, ou seja, se você classificar todos os dados como “não spam” acertará 60% das vezes. Essa taxa pode ser um bom indicador se o seu modelo funciona bem ou não quando comparada à precisão. Caso a taxa seja maior do que a precisão, podemos concluir que o modelo não está funcionando adequadamente para os dados;
• P-Value [Acc > NIR] = p-valor do teste unilateral onde a hipótese alternativa é: Accuracy > No Information Rate;
• Mcnemar’s Test P-Value = p-valor do teste de Mcnemar. O teste de Mcnemar é um teste não-paramétrico utilizado em dados nominais pareados. Para mais informações, consulte https://pt.wikipedia.org/wiki/Teste_de_McNemar;
• Prevalence (Prevalência) = \(\frac{VP+FN}{VP+FP+FN+VN}\);
• Pos Pred Value = \(\frac{\hbox{sensibilidade} \times \hbox{prevalência}}{\hbox{sensibilidade} \times \hbox{prevalência} + \left( 1- \hbox{especificidade} \right) \times \left( 1- \hbox{prevalência} \right)}\);
• Neg Pred Value = \(\frac{\hbox{especificidade} \times \left( 1- \hbox{prevalência} \right)}{\left( 1 – \hbox{sensibilidade} \right) \times \hbox{prevalência} + \hbox{especificidade} \times \left( 1 – \hbox{prevalência} \right)}\);
• Detection Rate (Taxa de Detecção) = \(\frac{VP}{VP+FP+FN+VN}\);
• Detection Prevalence (Prevalência de Detecção) = \(\frac{VP+FP}{VP+FP+FN+VN}\);
• Balanced Accuracy (Precisão Balanceada) = \(\frac{\hbox{sensibilidade} + \hbox{especificidade}}{2}\).